3.2.2.3 RAČUNANJE KOLIČIN V ZAPOREDNEM TOKOKROGU

KAZALO

    

 

 

3.2.2.3.1 Računanje nadomestne upornosti in prevodnosti

      
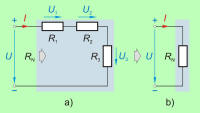
  Slika 3.2.2.3.1.1 prikazuje dejanski zaporedni tokokrog iz poskusa 3.2.2.1.1 in njegov nadomestni tokokrog z nadomestno (skupno) upornostjo zaporednih porabnikov RN. Napišimo enačbo napetostne zanke z ravnovesnima točkama na priključnih sponkah tokokroga:    

SLIKA

Slika 3.2.2.3.1.1: Zaporedni a) in nadomestni tokokrog b)

 

SLIKA

Slika 3.2.2.3.1.2: Zaporedni tokokrog

 
       
  U = U1 + U2 + U3    
  Napetosti na posameznem porabniku so po Ohmovem zakonu:    
  U1 = I · R1 , U2 = I · R2   in   U3 = I · R3    zato lahko zapišemo    
       
  U = I · R1 + I · R2 + I · R3    
      = I · (R1 +R2 +R3).    
       
 

Če na osnovi nadomestnega tokokroga (sl. 3.2.2.3.1.1) napišemo enačbo napetosti z upoštevanjem nadomestne upornosti, dobimo:

      
       
  U = I · RN      kar omogoča zapis enačbe:    
  I · RN = I · (R1 +R2 +R3)     in po deljenju obeh strani enačbe z I:    
  RN = R1 +R2 +R3    
       
 

Dobljeno enačbo nadomestne upornosti za tri porabnike lahko posplošimo v enačbo za nadomestno upornost poljubnega števila zaporednih porabnikov:

      
       
 
 

 

RN = R1 + R2 + R3 + ...

(Ω)   R1, R2, ... (Ω)
   
  Enačba 3.2.2.3.1.1    
       
 
► Nadomestna upornost zaporedno vezanih porabnikov je enaka vsoti upornosti posameznih porabnikov.  

 
       
  V primeru enakih upornosti R zaporednih porabnikov pa je skupna upornost:    
       
 
 

 

RN = n · R
(Ω)   n = število porabnikov; R ... (Ω)
   
  Enačba 3.2.2.3.1.2    
       
 
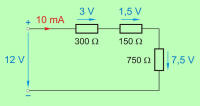
► Nadomestna upornost zaporedno vezanih porabnikov enakih upornosti je enaka produktu upornosti porabnika in števila porabnikov.  

 
       
  Nadomestna upornost zaporednega tokokroga s slike 3.2.2.3.1.2 je potem:    
       
  RN = R1 + R2 + R3 = 300 + 150 + 750 = 1200 Ω    
       
  Iz izračunane nadomestne upornosti in enačbe 3.2.2.3.1.1 lahko razberemo še uporabno zanimivost    
       
 
► Nadomestna upornost zaporedno vezanih porabnikov je vedno večja od največje upornosti zaporedne vezave.  

 
       
 

Tako kot je v vzporednih tokokrogih bolj praktično računati s prevodnostmi, je v zaporednih z upornostmi in nadomestno upornostjo. Če pa nadomestno prevodnost zaporednega tokokroga potrebujemo, jo izračunamo na že znani način:

      
       
 
  GN   = 1  
RN
(S)

RN(Ω)
   
  Enačba 3.2.2.3.1.3