|
|
 |
|
 |
 |
 |
 |
|
 |
|
|
 |
 Poskus
4.2.2.2.1: Poskus
4.2.2.2.1:
|
|
|
|
 |
Ponovimo
poskus 4.2.2.1.1 tako, da namesto vzporedne
vezave kondenzatorjev priključimo na izvor zaporedne vezave
(slika 4.2.2.2.2). |
 |
|
|
|
|
|
|
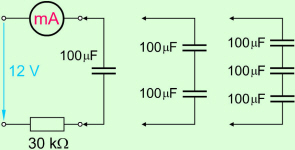
Slika 4.2.2.2.2 |
|
|
|
|
|
|
|
|
► |
Zaporedna vezava dveh, treh … kondenzatorjev
enakih kapacitivnosti se s povprečno enakim tokom polni
polovico, tretjino … časa polnjenja enega kondenzatorja. |
|
|
|
|
|
|
|
|
Poskus lahko ponovimo s kondenzatorji različnih
kapacitivnosti. |
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
► |
Zaporedna vezava kondenzatorjev sprejme manj elektrine
kot en kondenzator ali kondenzator z najmanjšo
kapacitivnostjo. |
 |
|
► |
Kapacitivnost zaporedne vezave kondenzatorjev je manjša
od najmanjše kapacitivnosti kondenzatorjev. |
|
 |
 |
|
|
|
|
|
|
|
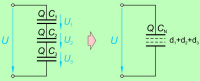
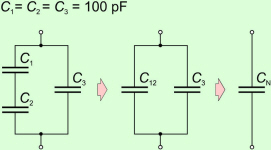
Tudi ta ugotovitev je logična, saj zaporedno
povezovanje kondenzatorjev pomeni povečevanje medsebojne
razdalje plošč kondenzatorja (slika
4.2.2.2.1). Čeprav ugotovitev
poskusa
4.2.2.2.1 pove veliko, ni dovolj natančna, zato si do splošnih
zakonitosti pomagajmo s premislekom, matematiko in
sliko
4.2.2.2.1. |
|
|
|
|
|
|
|
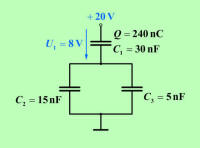
Napetost izvora povzroči naelektritev oblog
kondenzatorjev C1 in C3,
ki sta priključeni neposredno na sponki izvora z enakima elektrinama,
influenčni učinek pa poskrbi za enake elektrine tudi na drugih dveh
ploščah C1 in C3,
kakor tudi na ploščah C2. |
|
|
|
|
|
|
|
|
► |
Pri zaporedni vezavi kondenzatorjev so vsi kondenzatorji, ne
glede na kapacitivnost, naelektreni z enako elektrino. |
 |
 |
 |
|
|
|
|
|
|
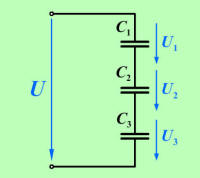
Napetosti na posameznem kondenzatorju so potem (enačba
4.2.1): |
|
|
|
|
|
|
|
|
U1 | = |
Q

C1 |
|
|
, |
U1 |
| = |
Q

C2 |
|
|
in |
U1 |
| = |
Q

C3 |
|
|
|
|
|
|
|
|
|
Na osnovi enačbe napetosti vezave na
sliki
4.2.2.2.1 lahko zapišemo: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I : Q |
|
|
|
|
|
|
|
U

Q |
|
= |
|
|
|
|
|
|
|
|
|
|
|
 |
|
(F-1) |
|
|
|
Enačba
4.2.2.2.1 |
|
|
C1(F); C2(F);
C3(F) |
|
|
|
|
|
|
|
|
► |
Obratna vrednost kapacitivnosti zaporedno vezanih
kondenzatorjev je enaka vsoti obratnih vrednosti
kapacitivnosti posameznih kondenzatorjev. |
 |
 |
 |
|
|
|
|
|
|
Pri zaporedno vezanih kondenzatorjih enakih kapacitivnosti velja: |
|
|
|
|
|
|
|
1

CN |
| = | |
| = | | n | · |
1

C |
|
|
|
ali |
|
|
|
|
|
|
|
|
|
 |
|
(F) |
|
|
Enačba 4.2.2.2.2 |
|
n = štev. zaporednih kondenzatorjev; C(F) |
|
|
|
|
|
|
|
|
► |
Kapacitivnost zaporedne vezave kondenzatorjev enakih
kapacitivnosti je enaka kvocientu kapacitivnosti enega
kondenzatorja s številom kondenzatorjev. |
 |
 |
 |
|
|
|
|
|
|
Primerjajmo napetosti na posameznih kondenzatorjih: |
|
|
|
|
|
|
|
U1

U2 |
|
= | |
|
= |
C2

C1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
► |
Zaporedna vezava kondenzatorjev razdeli napetost
izvora v obratnem sorazmerju s kapacitivnostjo
kondenzatorjev. |
 |
 |
 |
|
|
|
|
|
|
Prav gotovo smo ugotovili, da so zakonitosti, ki
veljajo za kapacitivnost vezave kondenzatorjev, analogne
zakonitostim, ki veljajo za prevodnost vezave uporov. |
|
|
|
|
|
|
|
Na splošno uporabljamo vzporedno, zaporedno ali tudi
sestavljeno vezavo kondenzatorjev kot nadomestni kondenzator s
kapacitivnostjo, ki z enim kondenzatorjem ni dosegljiva. |
|
|
|
|
|
 |
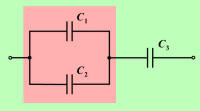
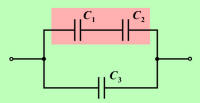
Sestavljene vezave kondenzatorjev so v praksi
redkejše, zato jih posebej ne bomo obravnavali. Z računanjem
kapacitivnosti sestavljene vezave pa ne bi smelo biti težav, saj ob
upoštevanju enačb za vzporedno in zaporedno vezavo kondenzatorjev
temelji na analogiji računanja upornosti sestavljene vezave uporov. |
|
|
|
|
|
|
|
Zaporedno vezavo kondenzatorjev uporabljamo tudi kot
delilnik napetosti, še posebej, kadar zaradi visokih napetosti v
električnem tokokrogu obstaja nevarnost preboja enega samega
kondenzatorja. |
|
|
|
|
|
 |
 Primer
4.2.2.2.1: Primer
4.2.2.2.1:
|
|
|
|
 |
Kolikšna je kapacitivnost vezave treh
kondenzatorjev s kapacitivnostjo 2,2 μF; 4,7 μF in 8 μF, če jih
povežemo a) vzporedno, b) zaporedno? |
 |
|
|
|
|
|
|
a) vzporedna: |
|
|
|
|
|
|
|
CN
= C1 + C2
+ C3
= 2,2 + 4,7 + 8 = 14,9 μF |
|
|
|
|
|
|
|
b) zaporedna: |
|
|
|
|
|
|
|
1

CN |
|
= | |
|
= | |
|
= | 0,454 + 0,213 + 0,125 |
|
|
|
|
|
|
|
|
1

CN |
|
= | 0,792 =>
CN |
| = |
1

0,792 |
|
| = |
1,26 μF |
|
|
|
|
|
|
|
 |
|
|
|
|
|
 |
 Primer
4.2.2.2.2: Primer
4.2.2.2.2:
|
|
|
|
 |
Zaporedna vezava kondenzatorjev 10 μF in 8 μF
(slika 4.2.2.2.3) je priključena na napetost 12 V. Izračunaj elektrino in
napetosti na kondenzatorjih! |
 |
|
|
|
|
|
|
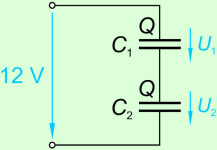
Slika 4.2.2.2.3 |
|
|
|
|
|
|
|
|
|
= |
1

10 |
| + |
1

8 |
|
|
|
|
= | 0,1 + 0,125 = 0,225 |
|
|
|
|
|
|
|
|
| CN |
= | 1

0,225 |
|
| = |
4,44 μF |
|
|
|
|
|
|
|
|
|
C | = |
Q

U |
|
|
=> |
|
Q = C ·
U
= 4,44 ·
10-6
· 12 = 53,3
µC |
|
|
|
|
|
|
|
|
|
|
|
C | = |
Q

U |
|
|
=> | U1 |
| = |
Q

C1 |
|
| = |
53,3 ·
10-6

10
·
10-6 |
|
| = | 5,33
V |
|
|
|
|
|
|
|
|
12 V =
U1
+ U2
=>
U2 =
12
-
5,33
= 6,67 V |
|
|
|
|
|
|
 |
|
|
|
|
|
|
 |
 Primer
4.2.2.2.3: Primer
4.2.2.2.3: |
 |
|
|
|
|
|
|
 |
 Primer
4.2.2.2.4: Primer
4.2.2.2.4: |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
   |
|
|