Gostota električnega toka. Če nosilci naboja prehajajo ploskev pravokotno, in tudi enakomerno po ploskvi, kar velja za »poprečni elektron«, ki prečka prerez ravnega vodnika (slika 1), potem gostoto električnega toka J na njej določa kvocient absolutne vrednosti toka i skozi ploskev in njena površina S:

 

Slika 1. Prosti elektroni prečkajo presek ravnega tokovodnika (v poprečju) pod pravim kotom.

Glede na pričakovani tok v žici in še sprejemljivo gostoto izbiramo primeren presek tokovodnika; v bakru (Cu) smatramo kot primerno tisto, ki ne preseže vrednosti 4 A/mm². Večja gostota povzroča prekomerno segrevanje; v takem primeru je potrebno vodnik hladiti z zrakom ali tekočino, sicer se poškoduje.[1]

Zgled 1. Vzdolž žice preseka 2,5 mm² je električni tok 8 A. Þ  Po enačbi je gostota električnega toka 3,2 A/mm² = 3,2 MA/m² (in ne presega štirih A/mm²).

Gostota toka in hitrost naboja. Vzdolž vodnika s presekom površine S naj se prosti elektroni premikajo s hitrostjo v. Na odseku dolžine Dl je določena množina naboja DQ s prostorninsko gostoto r = DQ / SDl. V času Dt = Dl / v se »gruča nabojev« premakne ravno za Dl (slika 2).

Po definiciji je tok i v vodniku v desno enak kvocientu DQ / Dt, zato je

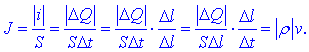
Pridobili smo ustreznejšo formulo za gostoto električnega toka, 

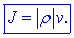
Zakaj? Gostota ni več vezana le na enakomeren prehod naboja skozi ploskev (kar je v resnici bolj izjema kot pravilo), ampak jo določa enostaven produkt, ki ima v splošnem v različnih točkah na ploskvi različne vrednosti. Primerov je veliko: tok skozi prevodnik poljubne oblike, ponikalni tok, kožni učinek v tokovodniku, vrtinčni toki v feromagnetiku idr.[2] Eden preprostejših je primer daljnovodne vrvi iz pletenice aluminijastih žic in nosilnega jeklenega stržena; vrvin tok se deli v pleteničin in strženov tok v razmerju njunih prevodniških lastnosti, zaradi česar je gostota toka na preseku vrvi gotovo neenakomerna.

Zgled 2. V bakru je število prostih elektronov enako številu atomov. Gostota prostih elektronov je n = 8,4×10²⁸/m³; pripadajoča prostorninska gostota elektrine je

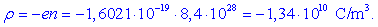
Rezultat preseneča: v litru oziroma (dm)³ bakra je množina proste elektrine enaka -13,4×10⁶ C. Določimo hitrost gibanja prostih elektronov v bakru, ko ima gostota toka v njem vrednost 4×10⁶ A/m². Þ  Iz zgornje enačbe sledi v = J / |r| = 300 mm/s. Presenetljivo: če bi (z)mogli opazovati gibanje elektrona, bi ta potreboval debelo uro, da bi se vzdolž vodnika premaknil za en meter.

Zgled 3. Enačba je primerna tudi za izračun gostote kakšnega drugega toka. Naj vleče burja skozi postojnska vrata s hitrostjo 150 km/h; gostota zraka je 1,2 kg/m³. Þ  Po enačbi je gostota zračnega toka burje 50 kg/(m²×s). Skozi plapolajočo vrečo odprtine 1 m² je pretok zraka 50 kg/s. Ni malo in nič čudnega ni, da tolikšen zračni tok prevrača kamione, razkriva strehe in lomi drevje.

Enačbo J = |r|v sporoča, da je gostota električnega toka sorazmerna hitrosti. Iz splošne fizike pa vemo, da je hitrost ena od tistih posebnih količin, ki je ne določa le iznos, izražen v m/s, ampak tudi smer in usmerjenost, zato bo nekaj podobnega verjetno veljalo tudi za gostoto električnega toka. Pa si poglejmo!