2.3.1 ODVISNOST TOKA OD ELEKTRIČNE NAPETOSTI

KAZALO

    

 

 

2.3.1.1 Električna upornost (R)

     
 

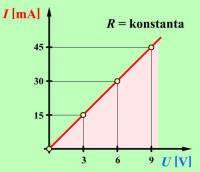
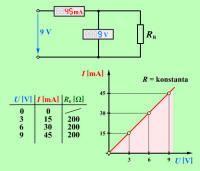
Na osnovi preglednice 2.3.1.1.1, ki povzema poskus 2.3.1.1, lahko ugotovimo zanimivo dejstvo:

 

ANIMACIJA

Animacija 2.3.1.1.1: Ohmov zakon; poskus 1
 

ANIMACIJA

Animacija 2.3.1.1.2: Ohmov zakon; poskus 2
 

ANIMACIJA

Animacija 2.3.1.1.3: Medsebojna odvisnost napetosti, toka in upornosti
 

FOTOGRAFIJA

Fotografija 2.3.1.1.1: Dekadni upor

 
       
 

Preglednica 2.3.1.1.1. Poskus 2.3.1.1 – razmerje U/I in I/U

U(V) I(mA) U/I (mA/V) I/U (mA/V)
3 15 3/15 = 0,2 V/mA 15/3 = 5 mA/V
6 30 6/30 = 0,2 V/mA 30/6 = 5 mA/V
9 45 9/45 = 0,2 V/mA 45/9 = 5 mA/V

U/I = 0,2 V/mA = konstanta

   
       
 

V našem primeru je za utiranje poti toku skozi porabnik za vsak mA toka potrebna napetost 0,2 V ali kar 200 V za 1 A. V bistvu smo tako »izmerili« zahtevnost poti za električni tok skozi porabnik.

    
       
►  

Napetost na enoto toka med sponkama porabnika imenujemo električna upornost1 porabnika. Označujemo jo z R.
► Električna upornost porabnika je določena s kvocientom napetosti na sponkah porabnika in toka skozi porabnik:  

 
       
 

R =

U
I
 (V/A)      I(A); U(V) 
   

Enačba 2.3.1.1.1: Definicijska enačba električne upornosti!
   
     
►  

Enota za merjenje upornosti je V/A. Je izvedena enota SI, imenujemo pa jo om (Ω)2, upornost pa tudi omska upornost.

     
  1 V / 1 A = 1 Ω    
     
 
►  

Če napetost 1 V med sponkama porabnika povzroči tok 1 A skozi porabnik, je upornost porabnika 1 Ω.

     
  Na osnovi definicijske enačbe za upornost porabnika lahko napišemo še enačbi:  
     
 

I =

U
R
 (A)      R(Ω); U(V) 

U =

I · R
(V)       (I/A)      I(A); R(Ω)   
 

Enačba 2.3.1.1.2

Enačba 2.3.1.1.3

 

  
     
 
►  

Električni tok skozi porabnik je premo sorazmeren z električno napetostjo na sponkah porabnika in obratno sorazmeren z električno upornostjo porabnika.

► Napetost, ki je potrebna za določen tok skozi porabnik, je premo sorazmerna s tokom in upornostjo porabnika.  

     
Enačbe 2.3.1.1.1, 2.3.1.1.2 in 2.3.1.1.3 omogočajo računanje upornosti, toka ali napetosti v električnem tokokrogu in predstavljajo enega od temeljnih zakonov elektrotehnike. Pravimo mu Ohmov3 zakon.  
     
Primer 2.3.1.1.1:

     
Primer 2.3.1.1.2:
     
Primer 2.3.1.1.3:
     
 

Praktično je, če si zapomnimo le eno, npr. enačbo 2.3.1.1.2, ostali pa, če ju rabimo, iz te izpeljemo.

  
     
   
 

1 Izraz upornost uporabljamo v tehniki, v fiziki pa pri nas upornosti pravijo upor

2 Velika črka grške abecede, omega

3 Georg Simon Ohm, nemški fizik in matematik