3.1.2.2 Tokovno vozlišče

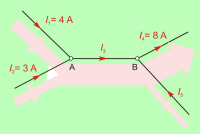
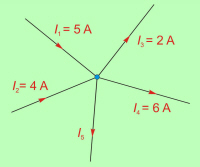
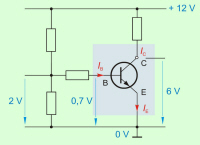
Slika 3.1.2.2.1 prikazuje splošni primer enostavnih tokovnih vozlišč. Na osnovi primera tokovnega vozlišča, ki ga prikazuje sl. 3.1.2.2.2 pa lahko zapišemo:

     Enačba 3.1.2.2.1

Dobljeni zakonitosti pravimo zakon tokovnega vozlišča ali tudi 1. Kirchhoffov¹ zakon. V splošni obliki ga zapišemo:

     Enačba 3.1.2.2.2

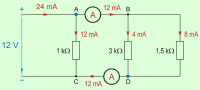
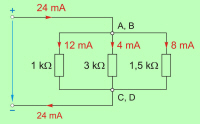
Pri računanju v vzporednih električnih tokokrogih bo koristno dejstvo, da lahko tokovna vozlišča, ki so na istem električnem potencialu (točki A in B ter C in D, sl. 3.1.2.2.3), brez škode združimo. Na ta način lahko nastane pomožna slika vezave porabnikov, ki je za vezavo iz poskusa 3.1.1 videti takšna, kot jo prikazuje sl. 3.1.2.2.3.

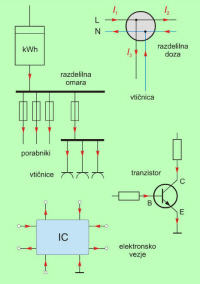
V praksi nastopajo tokovna vozlišča v električnih inštalacijah v obliki stičišč dveh ali več vodnikov (npr. v razdelilnih dozah), zbiralk v razdelilnih omarah in električnih naprav ter tri ali več polnih elektronskih elementov (npr. tranzistorjev), vezij in podobno (sl. 3.1.2.2.4).