|
|
 |
|
 |
 |
 |
|
|
3.2.2.2 Napetostna zanka
|
|
|
|
|
|
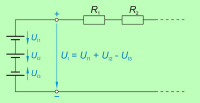
Pomembna ugotovitev dosedanje obravnave zaporednega
tokokroga je, da se napetosti na zaporednih porabnikih seštevajo. Pri
tem je pomembno opozoriti na dejstvo, da imajo napetosti na porabnikih
smer toka, torej isto smer (slika
3.2.2.1.1). |
|
|
|
|
|
|
|
|
|
|
|
|
► |
V zaporednem tokokrogu seštevamo napetosti iste smeri. |
 |
 |
 |
|
|
|
|
|
|
|
|
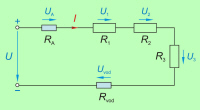
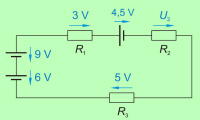
To je še posebej pomembno v primerih, ko imamo v
zaporednem tokokrogu več izvorov napetosti (slika 3.2.2.2.1), ki nimajo
vedno iste smeri. |
|
|
|
|
|
|
|
|
|
|
|
► |
V zaporednem tokokrogu se napetosti nasprotnih smeri med
seboj odštevajo. |
 |
 |
 |
|
|
|
|
|
|
|
|
Napetost 12 V na
slika 3.2.2.1.1 je napetost izvora in
predstavlja gonilno napetost električnega toka v tokokrogu. Napetost na
uporih (3 V, 1,5 V in 7,5 V) pa pove, kolikšen del gonilne napetosti je
potreben (uporabljen) za tok skozi posamezni upor. Po Ohmovem zakonu
vemo, da je za tok skozi porabnik potrebna napetost: |
|
|
|
|
|
U = I·R |
|
|
|
|
|
|
|
|
|
|
► |
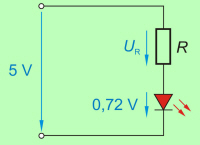
Napetostim na porabnikih zaporednega tokokroga (upornosti
porabnikov, vodnikov, merilnikov, ...
slika 3.2.2.2.2), ki so potrebne
za tok skozi te upornosti, pravimo tudi padci napetosti1. |
 |
 |
 |
|
|
|
|
|
|
|
|
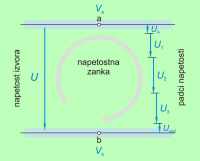
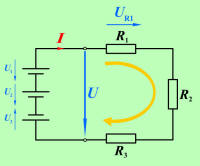
Napetost izvora (izvorov) in padcev napetosti vedno tvorijo zaključen in
uravnovešen sistem (slika 3.2.2.2.3). |
|
|
|
|
|
|
|
|
|
|
► |
Zaključenemu sistemu električnih napetosti izvorov in
porabnikov zaporednega tokokroga pravimo napetostna zanka. |
 |
 |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Zakon napetostne zanke: |
|
|
|
|
|
|
|
|
|
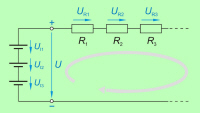
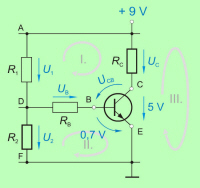
Na osnovi primera napetostne zanke zaporednega tokokroga (slika 3.2.2.2.4)
lahko zapišemo: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
► |
Vsota napetosti izvorov napetostne zanke (UI)
je enaka vsoti padcev napetosti (UR). |
 |
 |
 |
|
|
|
|
|
|
 |
Dobljeni zakonitosti pravimo zakon napetostne zanke ali tudi
drugi Kirchhoffov zakon. Zapišemo ga tudi v obliki: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Čeprav so napetostne zanke na prvi pogled značilnost
predvsem zaporednih tokokrogov, pa so prisotne v vseh, še tako
enostavnih tokokrogih z enim porabnikom ali zahtevnih sestavljenih
tokokrogih. Računanje z napetostnimi zankami pa je vedno v okviru
pravil, ki smo jih pravkar spoznali. |
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
 |
|
|
|
|
|
|
|
 |
|
 |
|
|
|
|
|
|
|
|
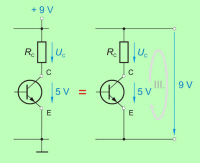
V praksi pa napetostne zanke niso vedno tako nazorne
kot v čistih zaporednih tokokrogih. Kot bomo videli v sestavljenih
tokokrogih, med elementi, ki jih zajame napetostna zanka, pogosto ni
izvora napetosti ali skozi elemente ni isti tok. Tudi za vse
take primere velja zakon napetostne zanke, le za
točki napetostnega ravnovesja2
zanke (slika 3.2.2.2.3) se moramo čim bolj praktično odločiti. |
|
|
|
|
|
|
|
|
|
|
|
► |
Za točki napetostnega ravnovesja napetostne zanke lahko izberemo
poljubni točki napetostne zanke, ki sta na različnih
električnih potencialih.. |
 |
 |
 |
|
|
|
|
|
|
 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 Pri nazivu
»padci« je možna analogija z vodnimi kaskadami.
2 Točki
uravnovešene »tehtnice« napetosti izvora/izvorov in padcev napetosti. |
|
|
|
|
|
|
|
|
|
   |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|