3.2.2.3 RAČUNANJE KOLIČIN V ZAPOREDNEM TOKOKROGU

KAZALO

    

 

 

3.2.2.3.3 Delitev napetosti

      
 

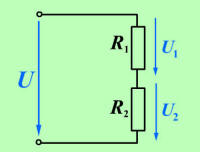
Pri ugotavljanju lastnosti zaporednega električnega tokokroga smo med drugim ugotovili, da se napetost izvora pri poganjanju toka skozi zaporedne porabnike, porazdeli na posamezne porabnike.

    

HITRE POVEZAVE

Zaporedna vezava linearnih bremen
 

SLIKA

Slika 3.2.2.3.3.1: Delitev napetosti na zaporedne porabnike enakih upornosti

 

SLIKA

Slika 3.2.2.3.3.2: Delitev napetosti na zaporedne porabnike različnih upornosti

 

ANIMACIJA

Animacija 3.2.2.3.3.1: Delitev napetosti
 
       
►   Zaporedna vezava porabnikov je delilnik napetosti.

 
       
 

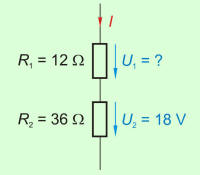
Primerjajmo razmerje padcev napetosti na porabnikih R2 in R3 tokokroga na sl. 3.2.2.3.2.1 (3.2.2.3.2.2) z razmerjem upornosti R2 in R3:

      
 
U2

U3
  =  
1,5 V

7,5 V
  =  
1

5
 
R2

R3
  =  
150 Ω

750 Ω
  =  
1

5
 
    
       
 
►   Zaporedno vezani porabniki delijo napetost v premem sorazmerju z upornostmi porabnikov.

 
       
  Do istega spoznanja pridemo tudi z matematično izpeljavo:    
       
 
U2

U3
  =  
I · R2

I · R3
  =  
R2

R3
    
   ali splošno:    
 
 
U1

U2
 =
R1

R2
   
 

 Enačba 3.2.2.3.3.1

    
       
 

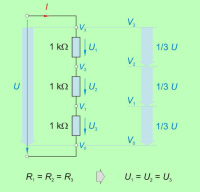
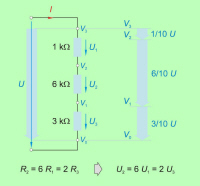
Spoznanja glede pravil deljenja napetosti na zaporedno vezanih porabnikih nazorno prikazujeta tudi sliki 3.2.2.3.3.1 in 3.2.2.3.3.2.

      
       
  K pridobljenim spoznanjem lahko tako dodamo še nekaj praktičnih dejstev:    
       
 
►   Na zaporedno vezanih porabnikih z enakimi upornostmi (sl. 3.2.2.3.3.1) je enaka napetost.
► Na zaporedno vezanih porabnikih z različnimi upornostmi (sl. 3.2.2.3.3.2) je na porabniku z najmanjšo upornostjo najmanjša napetost  
► Največji del napetosti izvora je v zaporedni vezavi vedno na porabniku z največjo upornostjo.  

 
       
Primer 3.2.2.3.3.1: