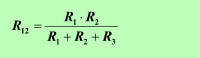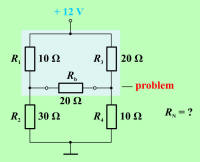
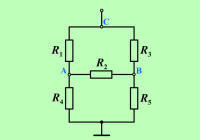
Idejno pot iz nerešljive vezave na sl. 3.5.1.1 v računsko nadomestno vezavo s čistimi zaporednimi in vzporednimi vezavami, katere nadomestno upornost znamo izračunati, prikazuje sl. 3.5.1.2.

HITRE POVEZAVE
Pretvorba zvezda-trikot

SLIKA
Slika 3.5.1.1: Skupna upornost mostične vezave

SLIKA
Slika 3.5.1.2: Prehod trikotne v zvezdno vezavo upornosti

SLIKA
Slika 3.5.1.3: Prehod trikotne v zvezdno vezavo upornosti

SLIKA
Slika 3.5.1.4: Pretvorba trikotne vezave v zvezdno

SLIKA
Slika 3.5.1.5: Trikotna vezava v zvezdno vezavo

SLIKA
Slika 3.5.1.6: Nadomestne upornosti mostične vezave z bremenom

ANIMACIJA
Animacija 3.5.1.1: Nadomestne upornosti mostične vezave z bremenom

ANIMACIJA
Animacija 3.5.1.2: Trikot > Zvezda (enačbe)

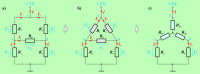
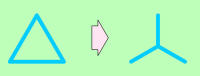
Slika sl. 3.5.1.2 b), električno gledano, slike sl. 3.5.1.2 a) ne spreminja in tudi problema ne zmanjšuje. Nudi pa obliko dela vezja, ki jo lahko vsaj poimenujemo. Pravimo ji trikotna vezava upornosti.

Na sliki sl. 3.5.1.2 c) pa je trikotna vezava zamenjana z zvezdno vezavo upornosti. Pomembno je, da taka zamenjava ohranja potenciale točk A, B in C ter vrednosti vseh količin preostalega dela vezja. Istočasno pa celotno vezje začasno (za čas računanja) dobi obliko, ki ima samo čiste zaporedne in vzporedne vezave upornosti.

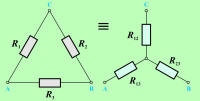
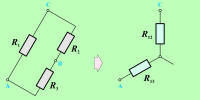
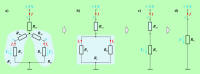
Poglejmo, informativno, kako dobimo enačbe za pretvorbo upornosti trikotne vezave v upornosti zvezdne vezave (sl. 3.5.1.3). Če naj vezavi zagotavljata enake električne potenciale točk A, B in C, morajo biti upornosti med točkama A in C, A in B ter B in C trikotne in zvezdne vezave enake. Zato za upornosti med točkama, npr. A in C obeh vezav (sl. 3.5.1.4), lahko zapišemo enačbo: