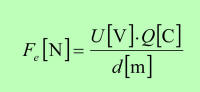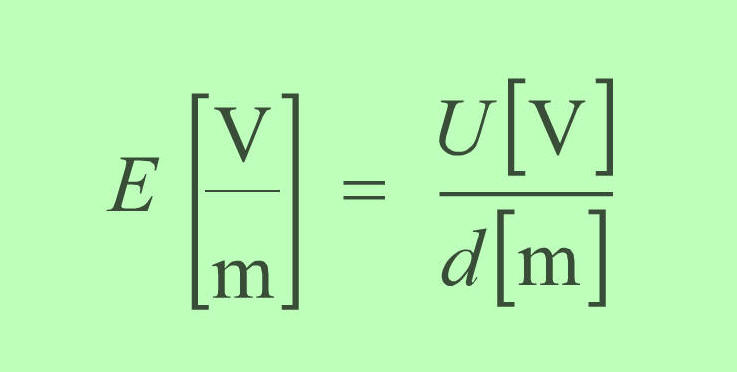|
|
 |
|
 |
 |
 |
 |
|
|
|
|
|
|
Poskus 4.1.2.1 pove, da je velikost sile na elektrino v
različnih točkah električnega polja lahko različna. Govorimo torej lahko
o različni jakosti oziroma o različni električni poljski jakosti v
različnih točkah električnega polja. Po dogovoru velja: |
|
|
|
|
|
|
|
|
|
|
|
|
► |
Merilo električne poljske jakosti je sila na enoto
elektrine. |
 |
 |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Enačba 4.1.2.1 |
|
|
|
|
|
|
|
|
|
Nekaj praktičnih primerov električne poljske jakosti prikazuje
preglednica 4.1.2.1. |
|
|
|
|
|
|
|
|
|
Preglednica 4.1.2.1: Električne poljske
jakosti |
|
|
|
|
|
|
Lokacija in situacija |
E(N/C) |
| |
jedro atoma urana |
3 x 1021 |
| |
v zraku pred strelo |
3 x 106 |
| |
ob bobnu fotokopirnega stroja |
105 |
| |
v Cu-vodnikih hišnih inštalacij |
10-2 |
|
 |
|
|
|
|
|
|
|
|
 |
Če upoštevamo, da elektrina nima smeri, ni težko
sklepati, da električni sili (F = Ε ∙ Q iz enačbe 4.1.2.1), poleg
predznaka elektrine, določa
smer
električna poljska jakost. |
|
|
|
|
|
|
|
|
|
|
|
► |
Smer električne poljske jakosti je enaka smeri električnih
silnic |
 |
|
► |
Električna poljska jakost je vektorska1 količina. |
|
 |
 |
|
|
|
|
|
|
|
i |
2Dogovorimo se, da bomo za električne količine, ki
imajo lastnosti vektorjev, na to le opozorili, zapis količine pa
bomo poenostavljeno pisali brez puščice. Smer vektorske količine ima
namreč odločujoči pomen pri razumevanju in računanju učinkov take
količine. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Homogeno in nehomogeno električno polje |
|
|
|
|
|
|
|
|
|
|
► |
Električnemu polju, ki ima v različnih točkah
prostora po velikosti in smeri enake poljske jakosti, pravimo
homogeno električno polje, v nasprotnem primeru pa
nehomogeno električno polje. |
 |
 |
 |
|
|
|
|
|
|
 |
Homogeno električno polje ustvarjata v prostoru med
seboj veliki, vzporedni, kovinski naelektreni plošči, ki sta si
dovolj blizu (sl. 4.1.1.3 d). Na osnovi primerov električnih polj na isti
sliki in poteka pripadajočih silnic lahko na splošno sklepamo: |
|
|
|
|
|
|
|
|
|
|
|
► |
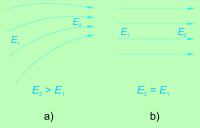
Homogeno električno polje prikažemo z
vzporednimi silnicami enake gostote, nehomogeno pa
s silnicami različnih gostot. |
 |
|
► |
Večja gostota električnih silnic pomeni večjo električno poljsko
jakost in obratno (slika 4.1.2.1). |
|
 |
 |
|
|
|
|
|
|
|
|
Določitev jakosti nehomogenih električnih polj je
zahtevna naloga, zato bomo obravnavali le homogena električna
polja. |
|
|
|
|
|
|
|
|
 |
 |
|
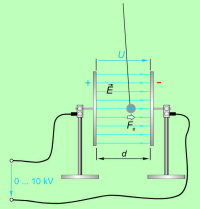
Med vzporedni kovinski plošči, ki sta na medsebojni razdalji
7 cm in priključeni na izvor nastavljive visoke napetosti,
obesimo na daljši vrvici z grafitom premazano namiznoteniško
žogico (sl. 4.1.2.2). Napetost izvora povečamo od 0 na 1,5 kV ter
z dotikom žogice ene od plošč žogico naelektrimo. Nato
povečujemo napetost izvora proti 7 kV: |
|
► Žogica se začne odklanjati iz mirovnega
položaja, in to tem bolj, čim višja je napetost med ploščama |
|
|
|
Poskus ponovimo tako, da pri razmaknjenih ploščah, npr. na 15 cm
in napetosti med ploščama na 7 kV, medsebojno razdaljo plošč
zmanjšujemo: |
|
► Naelektrena žogica se začne odklanjati,
njen odklon pa je tem večji, čim manjša je medsebojna razdalja
plošč. |
|
 |
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
► |
Električna poljska jakost med vzporednima
ploščama je tem večja, čim večja je napetost
med ploščama in čim manjša je njuna medsebojna razdalja. |
 |
 |
 |
|
|
|
|
|
|
 |
O tem se lahko prepričamo tudi po
matematični poti: |
|
|
|
|
|
|
|
|
|
Za prenos točkaste elektrine Q s plošče na ploščo
(sl. 4.1.2.2) je potrebno električno delo W = U ∙ Q ali enakovredno
mehansko delo W = Fe ∙
d. Z izenačitvijo desnih strani obeh izrazov
dobimo: |
|
|
|
|
|
|
|
|
|
|
| U · Q = Fe
· d => Fe = |
U
· Q

d |
|
|
|
|
|
|
|
|
|
|
|
Če dobljen izraz za silo na elektrino upoštevamo v
enačbi za električno poljsko jakost, dobimo: |
|
|
|
|
|
|
|
|
|
|
|
U
· Q

d · Q |
|
|
|
|
|
|
oziroma |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
► |
Električna poljska jakost homogenega
električnega polja je določena z napetostjo na enoto
dolžine električne silnice. |
 |
 |
 |
|
|
|
|
|
|
|
|
Na prejšnji strani smo spoznali enoto električne
poljske jakosti N/C, sedaj pa še V/m. Ugotovimo njuno medsebojno
povezavo: |
|
|
|
|
|
|
|
|
|
|
| Ws = J => VAs = Nm => | V

m |
|
| = |
| N

As |
|
| = |
| ali |
| = |
|
V

m |
|
= | N

C |
|
|
|
|
|
|
|
|
|
|
 |
|
 |
|
|
|
|
|
|
 |
|
 |
|
|
|
|
|
|
 |
 |
|
Kot zanimivost izračunajmo pospešek, ki
deluje na elektron v električnem polju iz naloge 2. Enačbo za
pospešek poznamo iz fizike, masa elektrona me pa je 9,11 · 10-31
kg!
|
a = | |
Fe

me
|
|
| |
| = |
|
|
6,4
· 10-15

9,11
· 10-31
|
|
| = |
| 7,02
· 1015 |
|
|
m

s
|
|
|
≈ |
| 0,72 · 1015g |
|
|
|
|
Ob upoštevanju, da smo z g označili
zemeljski pospešek, je pospešek na elektron tako velik, da si ga težko
predstavljamo. |
|
 |
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 vector, lat. –
nosilec
2 Fizikalnim
količinam, ki so določene z absolutno vrednostjo in smerjo (sila,
hitrost, … ) pravimo vektorji. Take količine označujemo s črko in
puščico nad črko, npr. E.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
  
|
|
|
|
|
|
|
|
|
|
|
|
|
|