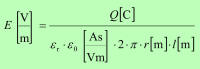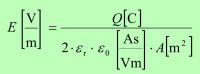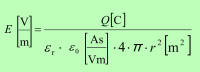4.1.5. NEPREVODNA SNOV V ELEKTRIČNEM POLJU

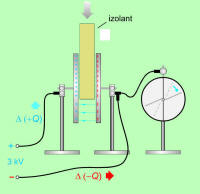
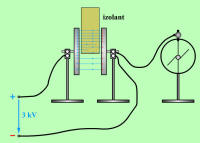
S povečanjem elektrine na kovinskih ploščah se je povečal tudi električni pretok med ploščama. Ker pa električne napetosti (vzroka za naelektrenje) med poskusom nismo spreminjali, lahko sklepamo:

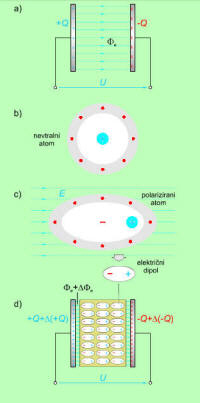
Pri pojasnjevanju ugotovitev poskusa 4.1.5.2 si lahko pomagamo s slikami 4.1.5.2 a, b in c.

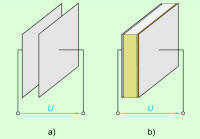
V izolantu, ki ni v električnem polju (sl. 4.1.5.2.a), se težišči pozitivne elektrine jedra in negativne elektrine elektronskega ovoja atomov prekrivata, zato so atomi navzven električno nevtralni. Ko pa izolant vstavimo v električno polje (sl. 4.1.5.2.b) se pod vplivom električnih sil težišči elektrin atomov elastično ločita. Tak atom za svojo okolico ni več električno nevtralen.

Pri nekaterih snoveh, npr. vodi, imamo pojav električnih dipolov na ravni molekule in sicer tudi, če snov ni v električnem polju.

Usmerjeni dipoli izolanta prispevajo dodatni električni pretok, ki pritegne dodatno elektrino na kovinski plošči (sl. 4.1.5.2.d).

Povečanje elektrine na kovinskih ploščah z dielektriki koristimo, kot bomo spoznali, za povečanje kapacitivnosti kondenzatorjev.

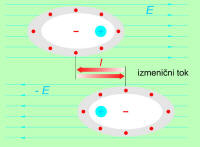
Če pa na kovinski plošči priključimo izmenično napetost, dobimo med ploščama izmenično električno polje, ki v notranjosti izolanta povzroči izmenično dielektrično polarizacijo. Posledica te je majhen izmenični tok v izolantu (sl. 4.1.5.3) in segrevanje izolanta. Takšno spreminjanje električne energije v toplotno je lahko koristno (varjenje umetnih snovi, sušenje lakiranih površin, mikrovalovne pečice ... ) ali škodljivo (npr. izgube energije v dielektriku kondenzatorja).

Krepitev električnega pretoka je zanimiva in lahko tudi koristna lastnost dielektrikov, zato jo spoznajmo nekoliko bolj. Najprej pa se seznanimo s povezavo med električno poljsko jakostjo E in gostoto električnega pretoka D v praznem prostoru:

Enačba 4.1.5.1

Konstanta dovzetnosti praznega prostora za električni pretok ε_o pove, kolikšno gostoto električnega pretoka v praznem prostoru povzroči enota električne poljske jakosti. Imenujemo jo dielektričnost praznega prostora, njena vrednost pa je ugotovljena z meritvijo:

Enačba 4.1.5.2

Če v električno polje vstavimo neprevodno snov, bo električni pretok sestavljen iz dveh delov:

1. iz električnega pretoka praznega prostora in
2. iz električnega pretoka, ki ga prispeva dielektrična polarizacija neprevodne snovi

Enačba 4.1.5.3

Faktor ε_r je faktor krepitve gostote električnega pretoka z dielektrikom. Pove, kolikokrat je gostota električnega pretoka v izolacijski snovi pri isti električni poljski jakosti večja od gostote pretoka v praznem prostoru. Imenujemo ga relativna dielektričnost. Nekaj primerov relativnih dielektričnosti podaja preglednica 4.1.2.

Preglednica 4.1.5.1: Relativna dielektričnost snovi

Produktu dielektričnosti praznega prostora in relativne dielektričnosti dielektrika pravimo kar dielektričnost dielektrika (ε).

Enačba 4.1.5.4

Dielektričnost je, podobno kot specifična električna upornost, snovna lastnost. Iz preglednice 4.1.2 je razvidno, da se zrak po dovzetnosti za električni pretok praktično ne razlikuje od praznega prostora (ε_r ≈ 1 → ε ≈ ε_o · 1 ≈ ε_o) medtem ko drugi izolanti krepijo električni pretok tudi večtisočkratno. Molekularni dielektriki imajo praviloma veliko večje relativne dielektričnosti od dielektrikov, v katerih nastanejo električni dipoli le pod vplivom električnega polja.

¹ di (lat.) = dve, electrum (lat.) = elektrika