|
|
 |
|
 |
 |
 |
 |
|
 |
|
|
 |
|
|
|
|
 |
Na enosmerno napetost 30 V priključimo prek
mA-metra z MO 1 mA kondenzator s kapacitivnostjo 100 μF ter
ocenimo tok in čas polnjenja kondenzatorja. Enako ponovimo s
vzporednima vezavama kondenzatorjev 2 x 100 μF in 3 x 100 μF (slika
4.2.2.1.2). Če pri poskusih uporabljamo iste kondenzatorje, jih pred
naslednjim poskusom razelektrimo prek upora 100 Ω. |
 |
|
|
|
|
|
|
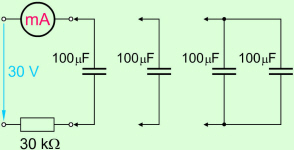
Slika 4.2.2.1.2 |
|
|
|
|
|
|
|
|
► |
Vzporedna vezava dveh, treh … kondenzatorjev
enakih kapacitivnosti se s povprečno enakim tokom polni
dvakrat, trikrat … toliko časa, kot en kondenzator. |
|
|
|
|
|
|
|
|
Poskus lahko ponovimo s kondenzatorji različnih
kapacitivnosti. |
|
|
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
Če upoštevamo, da je pri povprečno enakem toku
polnjenja vezav kondenzatorjev elektrina, ki jo sprejme vezava, premo
sorazmerna s časom polnjenja vezave kondenzatorjev, lahko sklepamo: |
|
|
|
|
|
|
|
|
|
|
► |
Elektrina, ki jo sprejme vzporedna vezava kondenzatorjev, je
enaka vsoti elektrin posameznih kondenzatorjev. |
 |
|
► |
Kapacitivnost vzporedne vezave kondenzatorjev je enaka
vsoti kapacitivnosti posameznih kondenzatorjev. |
|
 |
 |
|
|
|
|
|
|
|
|
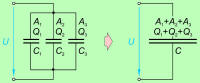
To je tudi razumljivo, saj vzporedno povezovanje
kondenzatorjev pomeni povečevanje površine plošč kondenzatorja
(slika
4.2.2.1.1). |
|
|
|
|
|
|
|
|
|
O ugotovljenem nas prepriča tudi matematika.
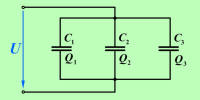
Vzporedno vezani kondenzatorji (slika
4.2.2.1.1) so priključeni na isto
napetost, zato lahko na osnovi enačbe
4.2.1 zapišemo: |
|
|
|
|
|
|
|
|
|
Q1 = U
·
C1
, Q2 = U
·
C2
in Q3 =
U
·
C3 |
|
|
|
|
|
|
|
|
|
Elektrine na kondenzatorjih mora zagotoviti izvor napetosti, zato: |
|
|
|
|
|
|
|
|
|
Q = Q1 + Q2
+
Q3 =
U
·
C1 + U
·
C2 + U
·
C3 , |
|
|
|
|
|
|
|
|
|
Q = U(C1 + C2
+
C3) I :
U. |
|
|
|
|
|
|
|
|
|
Q

U |
|
= | C1 + C2
+
C3 |
|
|
|
|
|
|
|
|
|
|
oziroma bo nadomestna kapacitivnost CN. |
|
|
|
|
|
|
|
|
|
|
|
 |
|
(F) |
|
|
|
Enačba
4.2.2.1.1 |
|
|
C1(F); C2(F);
C3(F) |
|
|
|
|
|
|
|
|
|
Pri vzporedno vezanih kondenzatorjih enakih kapacitivnosti velja: |
|
|
|
|
|
|
|
|
|
CN
= C + C
+ C + ... |
oziroma |
|
|
|
|
|
|
|
|
|
|
|
 |
|
(F) |
|
|
 Enačba 4.2.2.1.2 Enačba 4.2.2.1.2 |
|
n = štev. kondenzatorjev; C(F) |
|
|
|
|
|
|
|
|
|
|
► |
Kapacitivnost vzporedne vezave kondenzatorjev enakih
kapacitivnosti je enaka produktu števila kondenzatorjev
in kapacitivnosti enega kondenzatorja. |
 |
 |
 |
|
|
|
|
|
|
|
|
Primerjajmo elektrini na dveh kondenzatorjih: |
|
|
|
|
|
|
|
|
|
 |
Q1

Q2 |
|
= | U
·
C1

U
·
C1 |
|
| = | C1

C1 |
|
|
|
oziroma |
|
|
|
|
|
|
|
|
|
|
|
 |
|
|
|
|
 Enačba 4.2.2.1.3 Enačba 4.2.2.1.3 |
|
|
|
|
|
|
|
|
|
|
|
► |
Vzporedna vezava kondenzatorjev razdeli elektrino premo
sorazmerno s kapacitivnostjo kondenzatorjev. |
 |
 |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
  
|
|
|