6.1.2.1 Lenzevo pravilo elektromagnetne indukcije

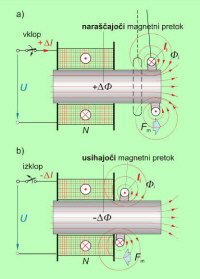
Po vklopu električnega toka je magnetni pretok tuljave moral narasti na vrednost Φ_m. Naraščajoči magnetni pretok tuljave je v sklenjenem ovoju induciral napetost, ki je v njem pognala kratkostični električni tok. Ta je v ovoju povzročil lastni magnetni pretok, za katerega lahko iz odbojne sile sklepamo, da je imel nasprotno smer kot naraščajoči magnetni pretok tuljave (ssl. 6.1.2.5 a) oziroma, da je nasprotoval naraščanju magnetnega pretoka tuljave.

Podoben učinek je imel inducirani magnetni pretok ovoja na usihajoči magnetni pretok tuljave po izklopu električnega toka. V tem primeru je inducirani magnetni pretok imel enako smer kot magnetni pretok tuljave (ssl. 6.1.2.5 b) in je nasprotoval usihanju magnetnega pretoka tuljave

Pričujoče pravilo je v skladu z naravno zakonitostjo težnje po ohranitvi energijskega ravnovesja, ki smo ga že omenili kot Lenzevo pravilo. Po tem pravilu lahko rečemo:

Ugotovljeno bomo v enačbi 6.1.2.1.1 splošnega indukcijskega zakona upoštevali tako, da bomo opustili zapis absolutne vrednosti inducirane napetosti, na desni strani enačbe pa bomo dodali » – «.

Enačba 6.1.2.1.1

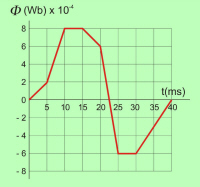
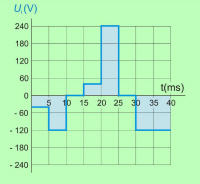
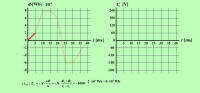
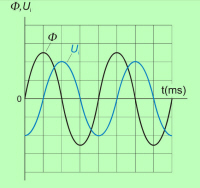
Iz primera je razvidno, da obliki časovnih potekov inducirane napetosti in magnetnega pretoka (sl. 6.1.2.6 in 6.1.2.7) v splošnem nista enaki. To pa ne velja za sinusno obliko (sl. 6.1.2.9):

Sinusni obliki napetosti bomo več pozornosti posvetili pri obravnavi izmeničnih tokov. Omenimo le zanimivo dejstvo, da se po sinusni zakonitosti spreminja pravokotna komponenta hitrosti prečkanja magnetnega pretoka pri rotacijskih generatorjih, sicer pa sinusno obliko izmenične količine ni enostavno dobiti.