Joulov zakon. Da bi Joulov zakon ustrezno osvetlili, se spomnimo trkov, do katerih prihaja, ko se nosilci naboja prerivajo skozi prevodno snov, oziroma sile upora, ki je električni ravno nasprotna. Vsak trk pomeni za delec izgubo njegove kinetične energije, ta pa se kaže v povečanju notranje energije snovi. Imejmo prevoden kanal, ki je priključen na vir napetosti U, skozi njega pa je elekrični tok jakosti I (slika 1). 

V intervalu Dt bo katerikoli presek kanala prečkala enaka monožina naboja DQ = IDt. Ravno tolikšna množina bo hkrati tudi vstopila in izstopila iz kanala in enaka množina naboja se bo premaknila tudi skozi vir. Če je tako, potem bo delo DA_e električnih sil v kanalu v času Dt enako vsoti produktov naboja DQ in delnih napetosti DU (potencialnih razlik, ki jih posamezni naboji DQ pretečejo), kar je enako tudi produktu naboja DQ in napetosti U, DA_e = DQU; to delo je hkrati enako tudi sproščeni toploti DW_t v kanalu oziroma delu DA_g neelektrične sile v viru, ki je v času Dt potisnila naboj DQ od negativne do pozitivne sponke:[1]

Preprosta enačba sporoča: sproščena množina toplote v prevodnem kanalu je enaka produktu napetosti, toka in intervala časa.

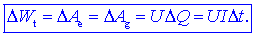
Zgled 1. Če priključimo grelec za vodo na vir napetosti 300 V, je skozi njega tok 15 A. Koliko toplote se sprosti v njem v 3 minutah? Þ Sproščena toplota je:

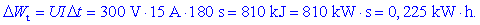
Elektrotehniki izražamo energijo najpogostejev kilo-, mega- ali gigavatnih-urah (za razliko od fizikov, ki izražajo delo ali energijo praviloma v džulih).