Gostota električnega toka. Če nosilci naboja prehajajo ploskev pravokotno, in tudi enakomerno po ploskvi, kar velja za »poprečni elektron«, ki prečka prerez ravnega vodnika (slika 1), potem gostoto električnega toka J na njej določa kvocient absolutne vrednosti toka i skozi ploskev in njena površina S:

 

Slika 1. Prosti elektroni prečkajo presek ravnega tokovodnika (v poprečju) pod pravim kotom.

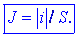
Glede na pričakovani tok v žici in še sprejemljivo gostoto izbiramo primeren presek tokovodnika; v bakru (Cu) smatramo kot primerno tisto, ki ne preseže vrednosti 4 A/mm². Večja gostota povzroča prekomerno segrevanje; v takem primeru je potrebno vodnik hladiti z zrakom ali tekočino, sicer se poškoduje.[1]

Zgled 1. Vzdolž žice preseka 2,5 mm² je električni tok 8 A. Þ  Po enačbi je gostota električnega toka 3,2 A/mm² = 3,2 MA/m² (in ne presega štirih A/mm²).

Gostota toka in hitrost naboja. Vzdolž vodnika s presekom površine S naj se prosti elektroni premikajo s hitrostjo v. Na odseku dolžine Dl je določena množina naboja DQ s prostorninsko gostoto r = DQ / SDl. V času Dt = Dl / v se »gruča nabojev« premakne ravno za Dl (slika 2).

Po definiciji je tok i v vodniku v desno enak kvocientu DQ / Dt, zato je

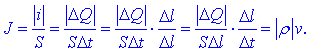
Pridobili smo ustreznejšo formulo za gostoto električnega toka, 

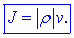
Zakaj? Gostota ni več vezana le na enakomeren prehod naboja skozi ploskev (kar je v resnici bolj izjema kot pravilo), ampak jo določa enostaven produkt, ki ima v splošnem v različnih točkah na ploskvi različne vrednosti. Primerov je veliko: tok skozi prevodnik poljubne oblike, ponikalni tok, kožni učinek v tokovodniku, vrtinčni toki v feromagnetiku idr.[2] Eden preprostejših je primer daljnovodne vrvi iz pletenice aluminijastih žic in nosilnega jeklenega stržena; vrvin tok se deli v pleteničin in strženov tok v razmerju njunih prevodniških lastnosti, zaradi česar je gostota toka na preseku vrvi gotovo neenakomerna.

Zgled 2. V bakru je število prostih elektronov enako številu atomov. Gostota prostih elektronov je n = 8,4×10²⁸/m³; pripadajoča prostorninska gostota elektrine je

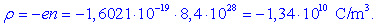
Rezultat preseneča: v litru oziroma (dm)³ bakra je množina proste elektrine enaka -13,4×10⁶ C. Določimo hitrost gibanja prostih elektronov v bakru, ko ima gostota toka v njem vrednost 4×10⁶ A/m². Þ  Iz zgornje enačbe sledi v = J / |r| = 300 mm/s. Presenetljivo: če bi (z)mogli opazovati gibanje elektrona, bi ta potreboval debelo uro, da bi se vzdolž vodnika premaknil za en meter.

Zgled 3. Enačba je primerna tudi za izračun gostote kakšnega drugega toka. Naj vleče burja skozi postojnska vrata s hitrostjo 150 km/h; gostota zraka je 1,2 kg/m³. Þ  Po enačbi je gostota zračnega toka burje 50 kg/(m²×s). Skozi plapolajočo vrečo odprtine 1 m² je pretok zraka 50 kg/s. Ni malo in nič čudnega ni, da tolikšen zračni tok prevrača kamione, razkriva strehe in lomi drevje.

Enačbo J = |r|v sporoča, da je gostota električnega toka sorazmerna hitrosti. Iz splošne fizike pa vemo, da je hitrost ena od tistih posebnih količin, ki je ne določa le iznos, izražen v m/s, ampak tudi smer in usmerjenost, zato bo nekaj podobnega verjetno veljalo tudi za gostoto električnega toka. Pa si poglejmo!

Skalarji in vektorji. Potrebe mehanike, kinematike teles in drugih vej fizike so narekovale vpeljavo pojmov in matematičnih sredstev, ki se navezujejo na vektorje. V čem je stvar? Za utež zadostuje podatek o masi, za talino podatek o temperaturi in podobno še za količine, kot so energija, čas, električna tok in napetost, moč idr. Takšnim rečemo, da so skalarne količine oziroma skalarji. Povsem nekaj drugega je hitrost. Meteorolog ne javi le hitrosti vetra, ampak tudi smer. Te vrste drugačnost velja tudi za silo. Trditev: na objekt z maso m deluje sila F, pove, da se objekt giblje s pospeškom F / m, nič pa kam. Smer gibanja je določena, če je znana smer sile. Tudi podatek o odmiku z mesta za korak ne pove dovolj; manjka še smer odkoraka. Kaj nam pomagajo sončne celice, če te ne bodo usmerjene proti Soncu. Zaključimo: fizikalna količina, ki je ne opredeljuje le mersko število in merska enota, ampak tudi smernost, je smerna količina; rečemo ji vektorska količina ali vektor.

Upodabljanje vektorjev. Glede na smernost se je za upodabljanje vektorske količine uveljavila usmerjena daljica: njena dolžina ustreza jakosti vektorske količine, nagib in puščica pa določata smernost količine. Ob konici pripišemo še simbol vektorske količine v pokončnem in krepkem tisku. Kot primer! Pri poševnem metu je tirnica gibanja telesa parabola; na njej je vektor hitrosti v tangenten na tirnico in vsakokrat drugačen. Dolžine usmerjenih daljic določa merilo, ki naj je izbrano tako, da je upodobitev pregledna (slika 3).

Komponente vektorja. Upodobitev vektorske količine z usmerjeno daljico je nazorna; manjka ji le še primeren matematični zapis, ki bo zajel smernost in jakost. Oboje (z)moremo izraziti v kartezičnem koordinatnem sistemu med seboj pravokotnih si osi X, Y in Z (slika 4).

Če usmerjeno daljico vektorja v v točki T (v prijemališču vektorja torej) opremimo z vzporednicami k osem, se izriše kvader z robovi, ki ustrezajo vrednostim pravokotnih projekcij v_x, v_y in v_z. Te nudijo pot nazaj k vektorju, in sicer tako, da »vektor sprejmemo kot trojko in da trojko sprejmemo kot vektor« na tale način: v = (v_x, v_y, v_z). S temi projekcijami oziroma komponentami smo »ugnali« smernost vektorja in našli možnost, da s pitagorsko vsoto komponent izrazimo tudi jakost, ki ji rečemo absolutna vrednost |v| = v vektorja v:

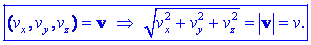
Absolutna vrednost vektorja ima vedno nenegativno vrednost, |v| = v ³ 0, medtem ko more imeti posamezna komponenta vektorja katerokoli realno vrednost. Če je katera od komponent vektorja negativna, pomeni to le to, da je usmerjena daljica nagnjena v nasprotno stran zadevne koordinatne osi.

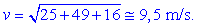
Zgled 4. Vektorju v = (5, -7, 4) m/s izračunajmo absolutno vrednost |v| = v! Þ  Po zgornji formuli je Vektor moremo predstaviti kot tri hkratna gibanja: s hitrostjo 5 m/s v smeri osi X, s hitrostjo 7 m/s v nasproti smeri osi Y in s hitrostjo 4 m/s v smeri osi Z. Vektor predstavlja poševno gibanje s hitrostjo 9,5 m/s.

Vektor gostote električnega toka. Od vektorja hitrosti do vektorja tokovne gostote J je le korak. Če se naboj s prostorninsko gostoto r giba vzdolž osi X s hitrostjo v_x, potem sta (v duhu enačbe J = |r|v ali |J_x| = |r||v_x|) na voljo izbiri J_x = ±rv_x. V skladu z dogovorom, da smer gibanja pozitivnega naboja določa usmeritev toka, izberemo J_x = rv_x; podobno postopamo tudi pri komponentah tokovnih gostot vzdolž osi Y in Z. Z združitvijo dobimo še vektorsko enačbo:[3]

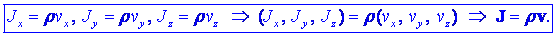
Absolutna vrednost J vektorja gostote toka J vrne zadevo v začetek:

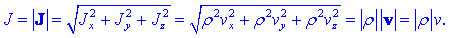
Pretočne cevke električnega toka.  Spoznali bomo grafični način, ki služi upodabljanju pretokov. Če smo se pri električnem toku oprli na podobnost z drugimi toki, izkoristimo to priliko še enkrat. Imejmo stekleno cevko, skozi katero črpalka žene tekočino s primešanim prahom. Delci rišejo v cevi sledi, nekakšne črte (krivuje). Enak vtis sproži vrtinčenje vode nad požiralnikom ali raznašanje listja v vetru. Slike ustvarjajo vtis nekakšnih »pretočnih cevk«, po katerih se »pretaka« voda ali zrak. Če narišemo nekaj teh cevk, nam njihove ograje oziroma gostotnice kažejo smer gibanja delcev v prostoru (slika 7).

Za tok vsake od cevk bi utegnili reči, da je v njo  na nek način ujet (zajet).

To grafično upodobitev si izposodimo tudi za tok elektrin! Čeravno je vodnik nekje tanjši, drugje debelejši, vmes tudi ukrivljen, je gibanje elektronov ujeto v namišljene cevke. Vsaka cevka ima svoj tok; njih vsota je enaka celotnemu električnemu toku v vodniku. Izgleda tako, »kot da bi bil vodnik narejen« iz tanjših žic, ki si celoten tok razdelijo med sabo; sliko cevk moremo opremiti še s puščicami (slika 8).

Verjetno je absolutna vrednost J vektorja tokovne gostote J večja tam, kjer je cevka ozka, in manjša tam, kjer je cevka razprta. Produkt površine preseka DS cevke in absolutne vrednosti J gostote toka na tistem mestu izraža tok Di skozi tisto cevko.