|
Prvi Kirchhoffov
zakon. Zakon je poseben primer kontinuitetne enačbe, ki velja v
primeru, ko se množina električnega naboja znotraj sklenjene ograje
ne spreminja; to (z drugimi besedami) pomeni, da je iS-P
enak nič. To pa še ne pomeni, da naboji ploskve S ne
prečkajo. Bodi tako, da na delu S1 ograje S
tok i1 izstopa, na delu S2 tok
i2 vstopa in enako tok i3 na
delu S3, na delu S4 pa tok i4
izstopa (slika 3).
Reči utegnemo: na
delu S1 izstopa tok i1, na delu
S2 izstopa tok -i2,
na delu S3 izstopa tok
-i3 in na
delu S4 izstopa tok i4. Kaj smo
naredili? S pomočjo predznaka smo dva toka preimenovali v izstopna,
da so potem vsi štirje toki izstopni. Celoten izstopni tok iP-S
je enak nič, obenem pa je iP-S tudi vsota delnih
izstopnih tokov, iz česar sledi:
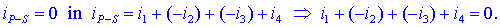
Če ugotovljeno
razširimo na n tokov, dobimo prvi Kirchhoffov zakon:
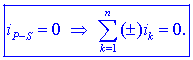
Zgled 3.
Imejmo primer treh žic, ki so spojene v točko in vodijo enosmerne
toke; skupno točk imenujemo spojišče ali razvejišče
(slika 4).
Z ampermetrom smo izmerili dva toka:
prvega v iznosu 1,75 A in drugega v iznosu
-0,5
A. Kolikšen je tretji tok?
Þ
Vsi toki so vstopni zato pišemo:
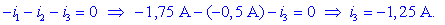
Tok tretje žice je negativen; to
pomeni, da iz P skozi njo izstopa tok 1,25 A.
Odločitev more biti tudi nasprotna: da ima izstopni tok predznak
»-«,
vstopni pa predznak »+«
(kar ne pomeni nič drugega kot množenje prejšnje enačbe s
številom
-1).
|