Napetost zanke in drugi Kirchhoffov zakon. Kaj vemo o delu električne sile? 1) Delo električne sile od ene do druge točke v prostoru je neodvisno od poti. 2) Delo električne sile po sklenjeni poti je enako nič. Vpeljali smo tudi električno potencialno energijo, električni potencial in električno napetost. Pa si izberimo sklenjeno krivuljo L in na njej pet točk s potenciali V_A, V_B, V_C, V_D in V_E (slika 11).

Napetosti med sosednjimi točkami so U_AB, U_BC, U_CD, U_DE in U_EA. Vpeljimo napetost zanke U_zanke; njo naj določa vsota napetosti vzdolž sklenjene poti v izbrani smeri (v levo ali desno). Ko izrazimo delne napetosti z razlikami potencialov, dobimo:

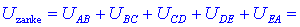
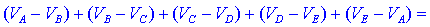
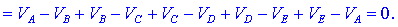
Pari potencialov se v celoti odštejejo; ugotavljamo sledeče: vsota napetosti v sklenjeni zanki je enaka nič, kar imenujemo drugi Kirchhoffov zakon:

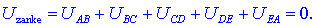
Glede na poljubnost označevanja napetosti med dvema točkama more biti katera od njih tudi negativno predznačena, kot na primer (slika 12):

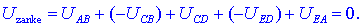
Prav zato zapisujemo drugi Kirchhoffov (zančni) zakon v splošnem takole:

 Pri tem pomenijo: s tekoči indeks splošne napetosti v sklenjeni zanki, znak »±« vsebuje dogovor, da imajo predznak »+« tiste napetosti, katerih označbe se ujemajo s smerjo obhoda po zanki, predznak »-« pa tiste, katerih označbe so nasprotne smeri obhoda po zanki.

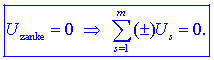
Zgled 10-2. Imejmo v prostoru pet točk: A, B, C, D in E (slika 13).

Dane so napetosti: U_AB = 5 V, U_CB = -3 V, U_CD = 7 V, U_BE = -4 V in potencial V_E = 0 V. Izračunajmo vse manjkajoče napetosti in potenciale! Za sklenjen obhod skozi točke A, B, C in D bomo pisali:

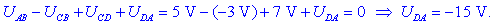
Od tod sledijo še potenciali:
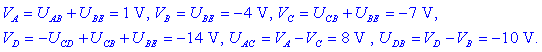