Mostično vezje. Na zagonetko mostične vezave elementov smo že opozorili, srečali pa smo jo tudi pri C-vezjih. Tam smo jo ugnali in ni razloga, zakaj je ne bi tudi v primeru mostiča uporov; to naj je vzbujano z virom napetosti U_g (slika 3).

V vezju označimo spojišča, vejne napetosti in toke; spojišče D naj je ozemljeno. Napetosti na uporih izrazimo s potenciali:

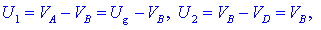
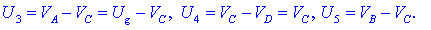
Zapišimo tokovni enačbi spojišč B in C:

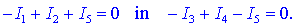
Da ne bo ulomkov, izrazimo toke s produkti prevodnosti uporov in napetosti, slednje pa s potenciali:

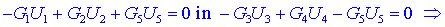
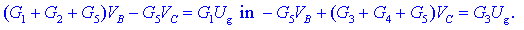
Dobili smo sistem dveh enačb z dvema neznankama, iz katerega moremo (pri znanih podatkih vezja) izračunati iskana potencala, napetosti in toke ter moči.

Zgled 2. Mostično vezje ima podatke: R₁ = 8 W, R₂ = 4 W, R₃ = 2 W, R₄ = 5 W in R₅ = 2 W ter U_g = 16 V. Izračunajmo potenciala, vse napetosti in toke ter moči! Þ V pripravljeni enačbi vstavimo podatke:

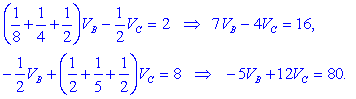
Sistem enačb rešimo kar z metodo nasprotnih koeficientov in dobimo:

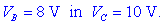
Od tu sledijo napetosti: U₁ = 8 V, U₂ = 8 V, U₃ = 6 V, U₄ = 10 V in U₅ = - 2 V; brž izračunajmo še toke: I₁ = 1 A, I₂ = 2 A, I₃ = 3 A, I₄ = 2 A in I₅ = - 1 A. Tok skozi vir je potemtakem 4 A in nadomestna upornost mostičnega vezja uporov je 4 W. Moči v posameznih uporih so po vrsti: 8 W, 16 W, 18 W,  20 W in 2 W. Seštevek moči je 64 W, kar potrjuje tudi produkt napetosti in toka vira.

Poseben primer mostičnega vezja je uravnovešen mostič, o katerem govorimo takrat, ko sta potenciala spojišč B in C enaka; takrat sta napetost in tok petega upora enaka nič. Kdaj se bo to zgodilo? V sistemu enačb uveljavljajmo zvezo V_B = V_C, pa imamo:

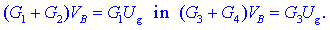
Kvocient levih strani enačb izenačimo s kvocientom desnih strani in smo že pri odgovoru:

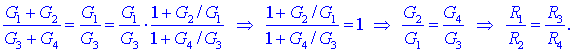
Mostično vezje bo v ravnovesju, ko bosta delilni razmerji zgornje in spodnje verige uporov enaki.