Pretvorba zvezda-trikot. V praksi srečujemo dve zanimivi tripolni vezji, ki ju sestavljata trojici uporov; to sta vezavi zvezda in trikot (sliki 4).

Če se ozremo na mostično vezje, vidimo, da tvorijo zvezdo prvi, drugi in peti upor, enako tudi tretji, četrti in peti, medtem ko tvorijo trikota prvi, tretji in peti ter drugi, četrti in peti. Pri vezavah nas bo zanimalo vprašanje: kdaj sta si vezji ekvivalentni? Spomnimo se nadomestne upornosti dvopola, čeravno včasih ne vemo, kaj se v njem v resnici skriva. To nas navaja na misel, da bi tudi od obeh vezav terjali: da sta nadomestni upornosti med enakima paroma sponk ene in druge vezave enaki. Če to zahtevamo, dobimo:

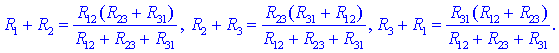
Ko tvorimo linearno kombinacijo izrazov, dobimo zvezo:

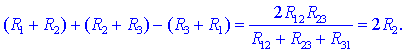
Na podoben način tvorimo še drugi dve in smo že pri enačbah, ki pretvarjajo upornosti trikotne vezave v upornosti vezave zvezda:

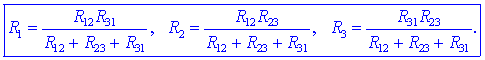
Možno pa je tudi obratno! Enakost imenovalcev ponuja zvezi:

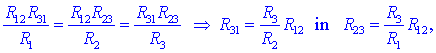
ki ju vstavimo v prvo od zgornjih enačb:

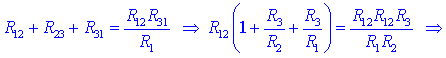
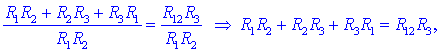
iz česar sledi R₁₂ in na podoben način tudi ostali dve:

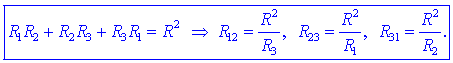
O simetrični zvezdi ali trikotu govorimo takrat, kadar so upornosti uporov v posameznih trojkah med seboj enake. Če je tako, potem je upornost upora v trikotu trikratnik upornosti upora v zvezdi: R_trikot = 3R_zvezda.

Zgled 3. Mostično vezje vsebuje upore upornosti R₁ = 8 W, R₂ = 4 W, R₃ = 2 W, R₄ = 5 W in R₅ = 2 W (podatki so enaki kot v zadnjem zgledu). Vprašajmo se po nadomestni upornosti vezja med sponkama (slika 5).

 Þ  Desni trikot, ki ga oblikujejo upori 4, 2 in 5 ohmov, pretvorimo v zvezdo uporov R_B, R_C in R_D. Če smiselno uporabimo izpeljane enačbe, sledi:

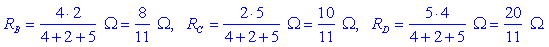
Nadomestna upornost dvopola bo sedaj:

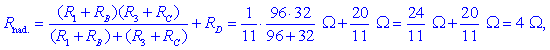
kar je enako rezultatu iz prejšnjega zgleda.