Realen napetostni vir. Spomnimo se baterije, akumulatorja, suhega člena in drugih, ki generirajo med elektrodama električno napetost. Kadar je tak vir neobremenjem, rečemo napetosti med elektrodama napetost odprtih sponk oziroma napetost prostega teka. V smislu predstavljenih strnjenih elementov električnih vezij bi utegnili viru prirediti neodvisen napetostni vir na primer izmerjene napetosti U_g, napetosti prostega teka, vendar temu ni povsem tako (slika 1).

 Zakaj ne? Priključimo na tak vir breme! Skozi porabnik bo tok I, med njegovima sponkama bo napetost U, in v njem se bo sproščala toplota z močjo IU (slika 2).

Enak električni tok bo obenem tudi skozi vir, zato se bo del toplote sproščal tudi v njemu. Če bi bil to npr. Voltov člen in bi imela elektrolitska posoda obliko kvadra dolžine l_g, ob nasprotnih stenah posode pa bi bili ploščni elektrodi površin S_g, bi imela notranja, električno prevodna pot od ene elektrode skozi elektrolit (svojske prevodnosti g_g) do druge elektrode notranjo upornost R_g = l_g / g_gS_g oziroma  notranjo prevodnost G_g = g_gS_g / l_g.

 Pri tem ni pomembna formula, ampak dejstvo, da ima tudi konduktivna pot skozi tak ali kakršenkoli drug vir v resnici tudi svojo električno upornost. Od tu sledi, da bo neelektrična sila v viru za prenos naboja IDt od ene do druge sponke opravila v času Dt delo U_gIDt, ki bo enako vsoti joulske toplote R_gI²Dt v viru in dela električne sile UIDt v bremenu. To zapišimo in okrajšajmo, kar se da:

 Dobili smo enačbo, ki povezuje napetost odprtih sponk vira, tok skozi breme in vir, napetost bremena in notranjo upornost vira. Prebrali bi jo tudi takole: napetost odprtih sponk U_g vira je enaka vsoti napetosti R_gI in napetosti U na bremenu. Zadnja enačba spominja na napetostno enačbo sklenjene zanke; v njej nastopajo napetosti v zanki toka I, ki je skupen viru in bremenu. Ponuja se prilika za njeno predstavitev v obliki enozančnega vezja koncentriranih elementov: neodvisnega napetostnega vira napetosti U_g, upora upornosti R_g in bremena; pridobili smo modelno vezje vezave bremena in vira (slika 3).

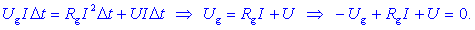
Modelno vezje napetostnega vira. Opredelitvi bremena se izogibamo in ne povemo, kaj je: ali je to linearen ali nelinearen upor ali nekaj čisto tretjega? To početje opravičujemo s tem, da nas trenutno zanimata zgolj vir in njegovo modelno vezje, podpira pa ga enačba, v kateri breme eksplicitno ne nastopa, zato ga zaenkrat tudi ne bomo risali, ampak le nakazali kot nekaj za črtkano mejo (slika 4).

Vidimo namreč, da se dva člena enačbe dotikata vira, to sta napetost odprtih sponk in notranja upornost. Zapišimo enačbo še drugače:

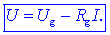
Dobili smo enačbo realnega napetostnega vira: napetost U (napetost med sponkama vira oziroma bremena) je za člen R_gI manjša od napetosti odprtih sponk U_g. Primer! Bodi napetost odprtih sponk suhega člena 1,5 V, njegova notranja upornost 100 mW, tok skozi njega in breme pa 200 mA. Napetost na bremenu bo 1,48 V; od napetosti prostega teka baterije bo manjša za 20 mV. Govorimo o notranjem padcu napetosti! Kaj to pomeni? Kadar bo tok skozi breme in vir večji, bo večji tudi notranji padec napetosti in posledično manjša bo napetost med sponkama vira oziroma bremena.

Karakteristika U-I. Vir označujeta dva podatka U_g in R_g = 1 / G_g! Iz enačbe vira izrazimo tok:

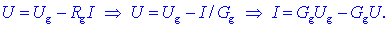
Dobili smo linearno enačbo, ki določa virovo karakteristiko U-I; upodablja jo poševna premica, katere nagib določa notranja prevodnost G_g (slika 5);

če bo ta večja (manjša notranja upornost), bo premica strmejša. Pritegneta še točki, v katerih premica seka abscisno (tokovno) in ordinatno (napetostno) os. Če je vir neobremenjen, I = 0 A, je napetost U enaka napetosti odprtih sponk U_o, U = U_o = U_g, ko pa bi bila bremenska upornost enaka nič, U = 0, da bi bili sponki vira »kratko« staknjeni, bi bil tok I enak toku kratkega stika I_k, I = I_k = G_gU_g. Pri napetostnem viru se točki kratkega stika izogibamo; zato smo se v pogojniku tudi izrazili. Zakaj? Notranja upornost napetostnega vira (baterije ali akumulatorja) je običajno relativno majhna; kratkostični tok bi bil gotovo izredno velik, kar bi moglo izzvati trajno uničenje vira. V izogib temu služi varovalka; ob prevelikem toku ta pregori, prekine tokokrog in obvaruje vir pred uničenjem (slika 6).

Dober in idealen napetostni vir. O solidnem napetostnem viru govorimo, če je njegova notranja upornost majhna, da je vrednost napetosti bremena zelo blizu vrednosti napetosti odprtih sponk, U = U_g - R_gI @ U_g, o idealnem pa takrat, kadar je notranja upornost enaka nič W (slika 7).

Idealu se zelo približajo posebna elektronska vezja, ki v področju pričakovanih vrednosti toka I zagotavljajo konstantno napetost med izhodnima sponkama.

Realen tokovni vir. Električni vir posreduje bremenu v resnici oboje, tok in napetost, zato je bolj stvar izbire, kako mu rečemo: ali tokovni ali napetostni vir. Resnično! Če člen G_gU_g, ki pomeni tok kratkega stika, označimo z I_g, bo enačba vira videti takole:
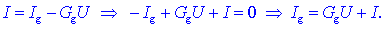