|
Maksimum moči.
Imejmo breme spremenljive upornosti, ki je priključeno na realen
napetostni vir (slika 4).
Vprašajmo se po
največji možni moči, ki jo more breme prejeti iz vira, oziroma po
moči, ki jo more vir posredovati bremenu. Moč P v bremenu,
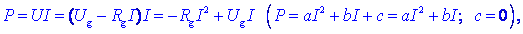
je kvadratična funkcija toka
z ničnim konstantnim členom. Navzdol obrnjena parabola ima ničli pri
I = 0 (odprte
sponke, ko je Rb
= ¥
W) in pri I
= Ug /
Rg (kratek stik, ko je Rb
= 0
W); koordinati točke T0
oziroma temena parabole, ki ustreza maksimumu moči v bremenu,
določajo koeficienti (a, b, c) parabole,
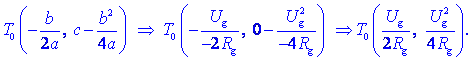
Maksimalna moč Pmaks.
= Ug2
/ 4Rg v bremenu je dosežena pri toku Ug
/ 2Rg, ki je tolikšen takrat, ko je upornost
bremena enaka notranji upornosti vira,
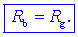
Breme je takrat
prilagojeno na vir; vir odda takrat vso razpoložljivo moč.
Bilanca moči v
enosmernem vezju. Zaključek
poglavja namenjamo vprašanjem moči. Kako je z njo v bremenu ali
viru, že vemo: določa jo produkt napetosti in toka. V nekaj zgledih
smo moči virov in bremen tudi izračunali ter ugotovili, da sta vsoti
enih in drugih enaki. Pri obremenjenem delilniku smo spoznali, da
razpoložljiva moč vira ni v celoti izkoriščena za moč v bremenu. V
enostavnem vezju smo se seznanili z delovno točko in njenim pomenom
za moč v bremenu, itn. Pa krenimo!
Ravnovesje
moči v električnem vezju. V
vezju označimo vejne toke, vejne napetosti pa tako, kot da bi bile
vse veje bremena (slika 1).
Ko tvorimo vsoto
produktov vejnih tokov in napetosti,
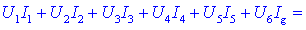
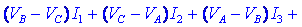 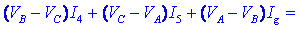
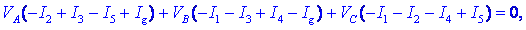
dobimo
presenetljiv rezultat, ki je posledica dejstva, da so izrazi v
oklepajih v resnici tokovne enačbe spojišč A, B in
C. Poglejmo na produkte še drugače:
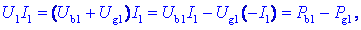
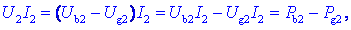
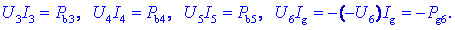
Produkt
napetosti in toka je enak razliki moči bremena in moči vira v veji;
če je v njej le vir, izostane moč bremena, in obratno. Ker pa je
vsota produktov vejnih tokov in napetosti enaka nič,
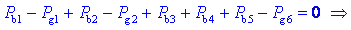 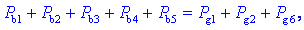
sledi:
v enosmernem vezju je vsota moči bremen enaka vsoti moči virov. Za
splošno vezje z n vejami bi se obe ugotovitvi glasili takole:
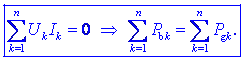
|