Gravitacijsko polje. Naj se v nekem trenutku kjerkoli na oddaljenosti r od središča Zemlje (z maso m) nahaja telo z maso m₁ (slika 1).

Slika 1. Vektor sile težnosti in vektor gravitacijskega pospeška.

Tam deluje na telo gravitacijska sila F_g jakosti F_g = Gmm₁ / r². Po drugem Newtonovem zakonu je kvocient sile F_g in mase m₁ enak gravitacijskemu pospešku g.[1] Ta je usmerjen k središču; njegova absolutna vrednost je g = F_g / m₁ = Gm / r². V g prepoznavamo vektorsko količino, ki je Zemlji lastna in daje informacijo o gravitacijskem polju okrog nje (slika 2).

Slika 2. Sredotežno polje gravitacijskega pospeška g.

Če je torej katerokoli telo sámo v prostoru, ga obdaja njemu lastno sredobežno gravitacijsko ali težnostno polje, ko pa se v tem polju znajde še drugo telo, deluje nanj tudi sila.

Zgled 1. Na oddaljenosti 2600 km od površine Zemlje je gravitacijski pospešek približno 5 m/s² (pol manj kot ob njeni površini). Če se tam nahaja vesoljska ladja z maso 3000 kg, deluje nanjo sila 15 kN, usmerjena k Zemlji, če pa tam plovila ni, tudi sile ni.

Vektor električne poljske jakosti. Ob električni sili smo izpostavili, da ima ima podobne lastnosti kot gravitacijska. Razlika tiči v dejstvu, da moreta biti sili na naboja privlačni ali odbojni, medtem ko sta težnostni zgolj privlačni. Brž ko si soseščino deli več nabojev, ima vektor rezultančne električne sile na izbran naboj Q določeno absolutno vrednost in smernost (slika 3).

Če bi Q nadomestili z nabojem -Q, bi se usmerjenost obrnila vsem delnim silam, in enako rezultančnemu vektorju, ki bi postal prejšnjemu nasproten: F_e ® -F_e. Podobno bi bilo tudi v primeru, ko bi naboj Q zamenjali z nabojem kQ; sila F_e bi prešla v silo kF_e. Ob takšnih zamenjavah ugotavljamo, da se kvocient sile in naboja ohranja: F_e / Q = -F_e / -Q = kF_e / kQ. Ti kvocienti ustrezajo normirani sili oziroma neki novi vektorski količini na tistem mestu, ki ni več v ničemer vezana na opazovano elektrino. Izkoristimo to lastnost in vpeljimo količino, imenovano vektor električne poljske jakosti E, na tale način:

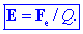
Ali nismo nekaj podobnega storili tudi v gravitacijskem polju? Seveda! Tam smo silo delili z maso, na katero deluje, in pridobili gravitacijski pospešek g oziroma normirano gravitacijsko silo. Od tu izhaja tale razvidna vzporednica: kar sporoča pospešek v polju sil težnosti, to sporoča električna poljska jakost v polju električnih sil.