Poljska jakost ploskovno porazdeljene elektrine. O ploskovnem naboju govorimo takrat, ko je ta razporejen po površini telesa.[1] Vzemimo zaenkrat primer ravne in tanke plošče enostranske površine S, na kateri je elektrina Q enakomerno razporejena.[2] Ves naboj naelektrene plošče je razpolovljen; pol naboja je na eni in pol na drugi strani.[3] Pri tanki plošči sta si steni zelo blizu, zato smemo govoriti o vsoti nabojev na enojni površini S. Vpeljimo gostoto ploskovno porazdeljene elektrine s, ki jo določa kvocient naboja in površine:

 Naelektrena plošča je v resnici ploskovni niz točkastih nabojev. Namišljeno jo razdelimo na majhne ploskvice površinic DS, na katerih so ustrezno majne množine naboja DQ = sDS (slika 15).

Za pridobitev rezultančne jakosti E je potrebno vektorsko sešteti prispevke poljskih jakosti teh, skorajda točkastih nabojev. To (sicer zapleteno) seštevanje da zelo enostaven rezultat. Končni vektor električne poljske jakosti enakomerno naelektrene plošče ima smer, ki je pravokotna na ravnino plošče, rečemo ji normalna smer. Komponento E_n, vstran od plošče usmerjene osi N, določa izraz:

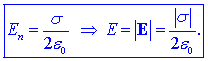
Rezultat je zanimiv. Pri točkasti elektrini je polje usihalo obratnosorazmerno kvadratu oddaljenosti, pri linijskem naboju obratnosorazmerno oddaljenosti, tu pa se sploh ne spreminja: jakost je scela konstantna. Takemu polju rečemo enovito ali homogeno polje. Kaj pa usmerjenost polja? Ko je naelektritev s pozitivna, ima normalna komponenta poljske jakosti pozitivno vrednost in vektor električne poljske jakosti je na obeh straneh plošče usmerjen vstran od nje, v nasprotnem pa k njej (slika 16).

Silnice električnega polja so v tem primeru kar vzporedne črte, usmerjene vstran ali k plošči (slika 17).

Da bi pa le ne bili preveč lahkomiselni, se moramo spomniti omejitve, da naj bo točka določanja polja relativno blizu glede na razsežnost plošče. Brž ko to omejitev prekršimo, tudi zgornji izraz več ne velja. Kako to mislimo? Če bo naelektrena plošča na primer disk premera 10 cm, točka določanja polja pa odmaknjena od nje vsaj nekaj milimetrov in vsaj kakšen centimeter stran od robu, potem je zgornja formula zelo ustrezna. V nasprotnem, ko bi bila točka računanja polja kakšnih 10 metrov stran od te plošče, bi disk s te razdalje ne bil več videti kot plošča, ampak že skoraj kot točka. Takrat bi, vsaj približno, smeli uporabljati že formulo za polje točkastega naboja.

Zgled 8. Ob steklo smo podrgnili tanko ploščo stiropora velikosti 1´50´100 cm. Bodi naboj na njej -500 nC. Kolikšna je poljska jakost ob površini, na oddaljenosti nekaj centimetrov od nje? Ploskovna gostota elektrine na njej je:

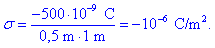
Uporabimo formulo za poljsko jakost in dobimo:

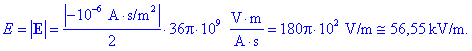
Vse drugače pa je daleč stran od plošče. Na oddaljenosti 20 m bomo poljsko jakost ocenili s formulo za jakost polja točkastega naboja:

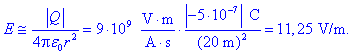
Vidimo občutno spremembo glede na bližnje polje. Ta ocena še dodatno podpira opozorilo, da je preprosta formula veljavna izključno v bližini plošče.

Lokalno homogeno polje. Čeravno je homogeno polje preprosto, nosi tudi splošno sporočilo. Ozrimo se na polja točkastih in linijskih nabojev. Njihova polja so nehomogena, spremenljiva tako po smeri kot po absolutni vrednosti. Vendar, če se v prostoru omejimo na nek manjši del, potem se v njem polje kaj bistveno ne spremenja; rečemo, da je tam lokalno homogeno (slika 18).

Ploščni kondenzator. Zares lepa lastnost električnega polja ob enakomerno naelektreni plošči kar kliče po primeru dveh enakih vzporednih plošč, ki sta si blizu in naelektreni z nasprotnima si nabojema ±Q (slika 19).

Zakaj? Iz ugotovitev o lastnosti polja naelektrene plošče se da zaključiti, da se bosta, izza plošč, vektorja delnih poljski jakosti E_Q in E_-Q nabojev Q in -Q odštela, saj sta tam enakih absolutnih vrednosti, vendar nasprotnih usmeritev, medtem ko se bosta med ploščama seštela v podvojen vektor poljske jakosti ene same plošče, saj imata enaki absolutni vrednosti in enaki usmeritvi (slika 20).

Da bi slednje jasno opredelili, vpeljemo pravokotno oziroma normalno os X, ki naj je po dogovoru usmerjena od plošče z nabojem Q k plošči z nabojem -Q. Komponenta E_x jakosti E med ploščama in njena absolutna vrednost sta:[4]

Rezultančno polje E med ploščama je homogeno: enake jakosti in smernosti. Ob tem se moramo nujno zavedati mejá veljavnosti preproste formule, ki sta opredeljeni podobno kot pri eni naelektreni plošči: formula velja v pasu med ploščama, ki pa ne seže povsem do robov (očrtkano področje). Tej omejitvi je zadoščeno brž, ko je razkorak d med ploščama majhen glede na izmere plošč, torej d << l₁, l₂. Električno polje med ploščama ponazarja tudi slika silnic, ki se raztezajo od ene do druge plošče (slika 21).

Sistem dveh vzporednih plošč imenujemo ploščni kondenzator. Če sta plošči nasprotno naelektreni, naelektreni z nabojema ±Q, govorimo o naelektrenem kondenzatorju. O njem bomo kasneje še marsikaj povedali. V tej ali v drugih izvedbah pomeni edenga od osnovnih gradnikov električnih vezij. Povedno je tudi njegovo ime; v smislu, da nekaj zbere, stisne, združi, kondenzira. Kot smo pred tem že ugotovili, ima sistem naelektrenih plošč lastnost, da zbere oziroma združi električno polje v prostor med ploščama.

Zgled 9. Leva plošča kondenzatorja leži v ravnini x₁ = 3 mm, desna pa v ravnini x₂ = 6 mm; plošči imata obliko diskov premera 10 cm. V medprostoru je poljska jakost, ki jo določa komponenta E_x = -300 kV/m. Izračunajmo vrednosti nabojev na diskih! Þ Leva plošča ima naboj Q, desna pa naboj -Q. Po formuli sledi:

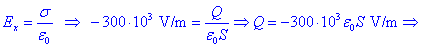
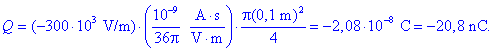
Negativen rezultat je pričakovan, saj je polje usmerjeno v levo.