Potenciali in napetost v naelektrenem ploščnem kondenzatorju. Imejmo sistem dveh naelektrenih plošč (slika 14).
 

Slika 14. Vrednost potenciala se vdolž osi X spreminja.

Naj je naboj Q₀ > 0 v točki T₁ s koordinato x₁. Ko bo stalna električna sila Q₀E_x = Q₀s / e₀ premaknila naboj Q₀ od točke T₁ do točke T₂ s koordinato x₂, bo (zaradi vzporednosti sile in poti) opravila delo A₁₂ = Q₀E_x(x₂ - x₁), pri premiku naboja od tod do točke T₀ s koordinato d, ki si jo izberimo kot referenčno točko električne potencialne energije, pa delo A₂₀ = Q₀E_x(d - x₂). Če je tako, potem sta električna potenciala v točkah T₁ in T₂ naslednja:
 

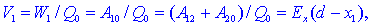
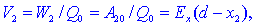
v vsaki drugi točki T (med ploščnama) s koordinato x pa je

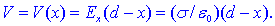
In kaj smo dobili? Potencial splošne točke podaja premica oziroma linearno padajoča funkcija vzdolž osi vektorja poljske jakosti E (slika 15).

Ker je tako, imajo točke z medploščne ravnine x = konstanta enak potencial; k tej se vzporedno nizajo še druge in vsaka od njih ima svoj električni potencial, zato jim pravimo ekvipotencialne ploskve ali kar ekvipotencialke.[1] Desna plošča kondenzatorja (x = d) je ekvipotencialna, s potencialom V_-Q = V₀ = 0 V (da ima tolikšnega, je posledica izbire točke T₀ za referenčno); enako leva (x = 0), s potencialom V_Q = E_xd, in tudi vmesne s potenciali vmesnih vrednosti.

 Kaže se zavedati dejstva, da vrednosti potencialov ekvipotencialnih ploskev ne pogojujeta zgolj razmak in električna jakost med ploščama, ampak tudi izbira mesta in končno tudi vrednost izhodiščnega potenciala. Tokrat smo si kot referenčno izbrali desno ploščo, mogli pa bi si tudi levo ali katero drugo vmesno vzporedno ploskev. V takšnem slučaju bi se nove vrednosti ločile od starih za aditivno konstanto oziroma za ± nekaj voltov. Da bi se izognili tej  nedorečenosti potencialov, govorimo pri naelektrenem kondenzatorju raje o napetosti U med ploščama, ki jo referenčno označimo in pišemo kot napetost od plošče z nabojem Q do plošče z nabojem -Q (slika 16).

Glede na sprejet dogovor, je napetost

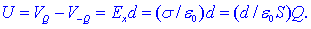
Napetost in naboj sta v sorazmernem odnosu; povezujeta ju dielektričnost in geometrija.[2] Enačba hkrati tudi preprosto poveže komponento poljske jakosti, razkorak in napetost med ploščama ter absolutno vrednost poljske jakosti. Če pa nas sama smernost poljske jakosti ne zanima, pišemo takole:

 
Zgled 3. Naelektren kondenzator ima med ploščama napetost 20 kV, razmik med njima je 1 cm, plošči pa sta kvadratni s površino 100 cm². Način označevanja geometrije naj je enak dosedanjemu. Določimo poljsko jakost, naboj na ploščah, gostoto naboja in lego štirih ekvipotencialk med ploščama! Þ Absolutna vrednost poljske jakosti je:

Gostoto naboja dobimo po že znani formuli:

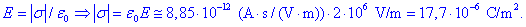
Absolutna vrednost nabojev na ploščah je:

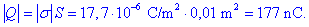
Leva plošča naj ima naboj 177 nC, desna pa naboj -177 nC. Če slednji dodelimo izhodiščni potencial nič voltov, ima leva plošča potencial 20 kV. Potencial med ploščama določa sledeča linearna funkcija:

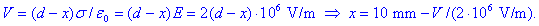
Najti želimo lege štirih ekvipotencialk, s potenciali 4, 8, 12 in 16 kV; po zgornji enačbi si njihove koordinate sledijo takole: x = 8, 6, 4 in 2 mm.