Električna influenca (eOET-1, nivo s3)

Vanj vstavimo nevtralno prevodno telo in se vprašajmo: kaj se utegne zgoditi?[1] V prvem hipu se v njem pojavijo sile na naboje: na protone sila eE₀, na elektrone pa sila -eE₀. Protonom se ne dogodi nič, saj so trdno v jedru atomov, atomi pa v kristalni strukturi snovi. Podobno je z elektroni na spodnjih lupinah. Edino, na kar zmoremo računati, so prosti elektroni. Ti se utegnjo pomakniti v nasprotni smeri polja, vendar ne tako, da bi jih nekaj z ene krenilo na drugo stran telesa, ampak tako, da se v to stran le rahlo zamaknejo. Na plati, od koder je polje E₀ naravnano, se zgodi presežek elektronov nad protoni, na plati, kamor je polje naravnano, pa se dogodi enak presežek protonov nad elektroni. Pojavu razdelitve pozitivnih in negativnih nabojev rečemo električna influenca; ob tem je še kar nekaj zadev, ki jih kaže razjasniti, zato pojdimo po vrsti!

Polje v prevodnem telesu. Zaradi premika prostih nabojev v prevodniku je upravičeno pričakovati, da se bo v celotnem prostoru vzpostavilo neko novo polje E, ki bo verjetno bolj ali manj drugačno, kot je bilo pred tem primarno polje E₀. Vprašajmo se: »kakšno« je polje E v prevodnem telesu? Zatečemo se k razmisleku, ki sloni na metodi protislovja. »Bodi polje E v prevodniku različno od nič!« Če je, se kanijo prosti elektroni (zaradi sile -eE) še naprej zgrinjati nekam ob steno telesa; posledično bi se množina naboja tam večala in večala, brez konca. Že, že, …, ampak to je v očitnem nasprotju s tem, da v omejenem prostoru ne more biti neomejeno mnogo delcev in zato tudi naboja ne. Sledi logični obrat! Vstopna trditev, »polje E v prevodniku je različno od nič«, je napačna, pravilna pa tale: polje E v prevodniku je enako nič; E = 0! Če pa je polje E v prevodniku ničelno, potem mora biti sekundarno polje E₁ oziroma polje influiranih nabojev v vseh točkah prevodnika ravno nasprotno polju E₀: E₁ = - E₀. Ali tudi: influenca nabojev ob površini prevodnika, ki se znajde v električnem polju, se zgodi v tisti »obliki in obsegu«, ki zagotavlja, da je rezultančna električna poljska jakost E = E₀ + E₁ povsod v prevodniku enaka nič (pri obliki in obsegu imamo v mislih predznak in gostoto naboja ob površini prevodnika).

Potencial prevodnega telesa. Če ugotavljamo, da je električno polje znotraj ničelno, da na naboje v prevodnem telesu ne deluje nikakršna električna sila, ki bi jih še mogla premakniti in opraviti delo, potem je razlika potencialov v dveh poljubnih točkah v telesu oziroma napetost med njima vedno enaka nič. Iz tega sledita ugotoviti: prevodnik je ekvipotencialno telo, njegova površina je ekvipotencialna ploskev.

Gostota influiranega naboja. Influirana elektrina se v prevodniku zbere tik ob površini; rečemo, da je tam naboj ploskovno porazdeljen.[2] Če je v polje umeščeno telo električno nevtralno, potem je množina naboja na eni strani telesa do predznaka enaka množini naboja na drugi strani.[3]

Polje izven prevodnega telesa. Če influirani naboji generirajo električno polje v prevodniku, ga zagotovo tudi zunaj! Kolikšno je, je odvisno od dveh dejavnikov: oblike telesa in porazdeljenosti influiranega naboja ob njegovi površini. Vsekakor je novo zunanje polje E spet vsota dveh: primarnega in sekundarnega polja.[4] Ko bi ju sešteli, bi bile silnice združenega polja takšne, da bi se nekatere od prvotnega primarnega polja rahlo upognile, nekatere bi se končale na strani negativnih influiranih nabojev, spet druge pa bi se začele na strani pozitivnih influiranih nabojev. Ker pa je površina ekvipotencialna ploskev, so silnice polja na njo gotovo pravokotne (slika 2).

Poljska jakost tik ob prevodniku. Spomnimo se električnega polja med in za ploščama ploščnega kondenzatorja. Če se (kot opazovalci) premaknemo izza plošče, kjer ni polja, pred ploščo, kjer ima polje znano jakost E_n = s / e₀, potem opažamo preskok vrednosti poljske jakosti z vrednosti nič na vrednost s / e₀. Ali ni morda nekaj takega tudi pri poljski jakosti ob površini telesa, saj moremo vsako ovalno površino telesa v njegovi neposredni bližini smatrati za lokalno ravno? Resnično: polje v prevodniku je ničelno, tik nad površino pa ima poljska jakost vrednost E_n = s / e₀. Če je gostota naboja tam pozitivna, je vektor električne poljske jakosti usmerjen iz prevodnega telesa, sicer pa v njega (slika 3).

Pojav influence pri naelektrenem telesu. Če je telo predhodno naelektreno z nabojem, se po vnosu v električno polje tudi njemu »zgodi« prerazporeditev prostih elektronov. Električno polje v njem je iz istega razloga spet ničelno in presežni naboj je ponovno le ob površini telesa. Tudi relacija med poljsko jakostjo ob površini prevodnika in gostoto ploskovno porazdeljene elektrine ostaja enaka.

Naelektreno prevodno telo. Nov primer bi bil, da je naelektreno telo samo v prostoru, primarno polje pa je enako nič. Polje v prevodniku mora biti spet enako nič, presežni naboj pa le ob njegovi površini. Zanj utegnemo reči, da je razporejen tako, da je električna poljska jakost povsod v notranjosti ničelna.

Naelektrena krogla. Z nabojem Q naelektrena prevodna krogla polmera a je lep primer samega prevodnega telesa. Pri njej ni težav! Ni namreč razloga, da bi naboj ob površini ne bil enakomerno porazdeljen; z gostoto s = Q / 4pa². Ob površini je zato normalna oziroma radialna komponenta poljske jakosti E naslednja: E_r = E_n = s / e₀ = Q / 4pe₀a². Izraz spominja na polje E_r točkastega naboja na oddaljenosti a. Sklepati moremo, da je poljska jakost tam tolikšna, kot da bi bil kroglin naboj Q združen v njenem središču, v zgolj navideznem naboju »Q«, ki je (kot se pokaže) hkrati tudi v vlogi neke vrste nadomestnega vira za polje kroglinega naboja v zunanjosti (slika 4).

Res: na oddaljenosti r od centra krogle je radialna komponenta poljske jakosti določena takole:[5]

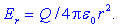
Naelektren raven vodnik. Vodnik polmera a in dolžine l naj je naelektren z z nabojem Q = ql; na plašču je s = Q / 2pal = q / 2pa; poljska jakost v njem je ničelna. Normalna, radialna komponenta poljske jakosti ob plašču vodnika je E_r = E_n = s / e₀ = q / 2pe₀a; izraz spominja na jakost v okolici linijskega naboja. Sklepamo: poljska jakost ob vodniku je tolikšna, kot da bi bil celoten obpovršinski naboj združen v osi vodnika v linijski naboj »q« (slika 5).

Ta je ponovno le v vlogi nadomestnega vira. Na oddaljenosti r od osi vodnika je radialna komponenta vektorja poljske jakosti določena s preprosto formulo:

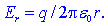
[1] Pričakovana sprememba se izvrši izredno hitro. Čas prilagoditve na nove razmere je reda velikosti relaksacijskega časa, ki je za kovine okoli 10^-14 s (za druge snovi tudi mnogo daljši).

[2] Presežek elektrine se nahaja v sloju debeline nekaj Å. Račun pokaže, da ima morda le vsak milijonti obpovršinski atom višek ali primanjklaj elektrona. To pomeni, da sloj influiranih nabojev sploh ni tako gost, kot bi morda prvi hip pričakovali.

[3] To sporoča tudi zakon o ohranitvi električnega naboja: v prostor ujeta množina naboja je nespremenljiva, more pa se prerazporediti; pri električni influenci je na delu ravno to.

[4] Določanje sekundarnega polja influiranih nabojev je težje opravilo, ki se mu moramo tu žal izogniti.

[5] Ker je jakost polja v prevodni krogli ničelna, moremo sklepati tudi obratno: če je po površini krogelne lupine naboj razporejen enakomerno, je njegovo električno polje v krogli enako nič. Navežimo se na gravitacijsko polje Zemlje. Tudi zanj velja podobno: gravitacijski pospešek ob Zemljini površini je tolikšen, kot da bi bila stisnjena v središče, v masno točko. Nadaljujmo še s privzetkom, da je Zemlja »lupina«; da je enake mase, vendar izvotlena. V zunanjosti bi se to ne odrazilo, v »luknji« pa bi bil pospešek enak nič; v luknji bi predmeti lebdeli.