Električno povezovanje kondenzatorjev.  Dva ali več kondenzatorjev tudi »združujemo«: električno jih povezujemo v zaporedne (serijske), vzporedne (paralelne) in sestavljene vezave. Na ta način tvorimo vezje kondenzatorjev; rečemo mu kondenzatorsko ali C-vezje. S povezovanjem njihovih priključkov nastajajo spojišča in zanke vezja. Na takšna vezja priključujemo tudi vire, ki izvršijo naelektritve kondenzatorjev oziroma prerazporeditve prostih nabojev med ploščami.

Kondenzatorska vezja. Do tu so bila vezja preprosta. Spoznali smo primere vzporedno, zaporedno in sestavljeno povezanih kondenzatorjev. Računanje ni delalo težav, kar še ne pomeni, da moremo na enak način ugnati vsako drugo vezje. Hitro se da najti primere, v katerih se ne znajdemo dobro, zaplete se, če je v vezje vključenih več virov, ali celo, da vlogo vira prevzame kak drug, predhodno naelektren kondenzator. V nadaljevanju bo beseda ravno o tem, predvsem pa o metodi, ki omogoča analizo takšnih vezij.

Spojiščna metoda. Metoda spojiščnih potencialov sloni na znani ali privzeti vrednosti električnega potenciala vsaj enega spojišča v vezju; no, privzeti ga smemo že zato, ker je to v duhu možne izbire točke izhodiščnega potenciala. Moremo se opreti tudi na prakso, da je eno spojišče vezja (že zaradi varnosti)  praviloma ozemljeno. Najbolje bo, da se z metodo spoznamo v vezju, ki bi ga znali razrešiti že na podlagi dosedanjih znanj (slika 1).

Simbol ozemljitve kaže, da je potencial V_C = 0 V, spojišču A pa določa potencial napetost vira, V_A = U; če nam uspe določiti potencial V_B, sledijo napetosti že kar iz njih:
 

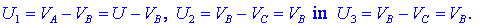
V spojišče B povezane plošče predstavljajo nevtralno telo, kar pomeni, da je njihov celotni naboj po priklopu vira, ki izvrši le prerazporeditve nabojev, še vedno nič kulonov. In natančno v tem tiči srž metode spojiščnih potencialov. Torej! Zapišemo nevtralnost telesa B, naboje pa izrazimo s produkti zadevnih kapacitivnosti in napetosti,
 

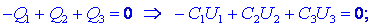
napetosti izrazimo s potenciali in enačbo uredimo, 
 

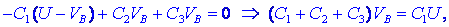
pa smo že pri iskanem potencialu: 

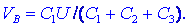
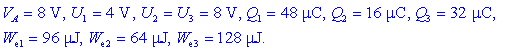
Zgled 1. Podatki vezja so: C1 = 12 mF, C2 = 2 mF in C3 = 4 mF ter U = 12 V. Izračunajmo vse! Þ Po izpeljani formuli in ostalih zvezah bodo: Iz izračunanih vrednosti vidimo, da je skozi vir stekel naboj Q1 = 48 mC, vir pa je zvezju kondenzatorjev posredoval energijo 288 mJ.

Mostično vezje. Ime izhaja iz oblike vezja; vodoravna veja, v kateri je peti kondenzator, spominja na brv ali most (slika 2).

 Vezje je zagonetno zato, ker ne prepoznamo, da bi bil vsaj kateri kateremu vzporeden ali zaporeden; da bi takšna dva računsko združili v enega in si vezje nekoliko poenostavili. Ako bi ne bilo petega kondenzatorja, tudi težav ne bi bilo, tako pa verjetno so, vendar jih bomo zmogli! Kako? Označimo spojišča in elemente vezij ter izrazimo napetosti kondenzatorjev z razlikami potencialov,

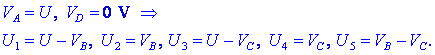
V spojišče B povezane plošče kondenzatorjev so prvo, v spojišče C povezane plošče pa drugo nevtralno telo. Za njiju zapišimo zakon o ohranitvi elektrine,

naboje izrazimo s produkti njihovih kapacitivnosti in napetosti,

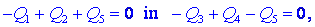
 napetosti zamenjamo z razlikami potencialov,

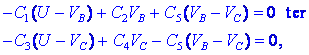
 in enačbi uredimo,

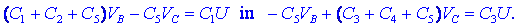
Dobili smo sistem dveh enačb z dvema neznankama; če poznamo napetost vira in vse kapacitivnosti, moremo izračunati iskana potenciala, nato pa še napetosti, naboje in energije v kondenzatorjih.

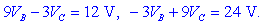
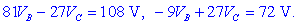
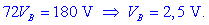
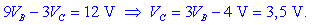
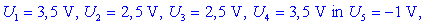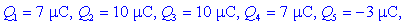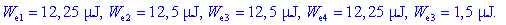
Zgled 2. Podatki so: C1 = C4 = 2 mF, C2 = C3 = 4 mF in C5 = 3 mF ter U = 6 V. Izračunajmo spet vse! Þ Podatke vstavimo v zgornji enačbi: Rešimo ju z metodo nasprotnih koeficientov. Prvo množimo z 9, drugo pa s 3: Če seštejemo levi strani enačb in to izenačimo z vsoto desnih strani, dobimo: Preostane še potencial spojišča C: Od tu dobimo napetosti, naboje in energije: Vir je prenesel naboj, ki je vsota nabojev na prvem in tretjem kondenzatorju, kar da 24,75 mC. Od tu sledi nadomestna kapacitivnost mostičnega vezja: 4,125 mF.

Vezje z dvema viroma. Kondenzatorsko vezje more imeti tudi več virov. Bodi vezje treh kondenzatorjev in dveh virov (slika 3).

 Poiščimo enačbo, ki bo določila potencial spojišča A! Pišemo po ustaljenem postopku! Najprej zakon o ohranitvi naboja,

nato izrazimo še napetosti s potenciali in smo že pri koncu:

Zgled 3. Podatki so: C1 = 1 nF, C2 = 2 nF C3 = 3 nF, U4 = 4 V in U5 = 5 V. Izračunajmo spet vse! Þ Pišimo: Od tu dobimo napetosti, naboje in energije: Negativna vrednost druge napetosti in naboja ne pomeni nič drugega kot to, da je v resnici naelektritev tega kondenzatorja ravno nasprotna označeni.

Elektritev z naelektrenim kondenzatorjem. Omenili smo, da (z)more biti kondenzator tudi vir, kadar se prazni. Primer bodi kar najbolj preprost! Naj je kondenzator kapacitivnosti C₁ predhodno naelektren z nabojema ±Q₀, da ima napetost Q₀ / C₁, drugi, kapacitivnosti C₂, pa naj je prazen (slika 4).

Po sklenitvi stikala se del elektronov od spodnje leve plošče pomakne k desni spodnji plošči, od desne zgornje pa enak del elektronov k levi zgornji plošči. Po novem sta na levem kondenzatorju naboja ±Q₁, na desnem pa naboja ±Q₂. Določimo jih! Po prerazporeditvi bosta napetosti kondenzatorjev enaki in vsota novih nabojev bo enaka prejšnjemu naboju:

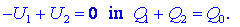
Nova naboja izrazimo z napetostima in smo že pri koncu:

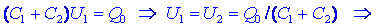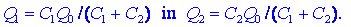
Naboj Q₀ se razdeli v dva dela, sorazmerna kapacitivnostma. Stanje napetosti in nabojev je takšno, kot da bi bila kondenzatorja vezana vzporedno, sicer pa ne vemo, kako sta. Nekdo bi utegnil reči, da sta vezana zaporedno, pa kljub temu ni v zmoti. Pojma vzporednost in zaporednost se sicer »majeta«, enačbe in fizikalna dejstva pa nič.[1]