Zaporedna vezava kondenzatorjev. V verigi naj so le trije kondenzatorji; točke spojišč označimo z A, B, C in D (slika 7).

Ko med krajni točki A in D priključimo vir napetosti U, izvrši ta prerazporeditev nabojev na ploščah. Le kako!? V kratkem času elektrenja potisne vir od skrajno spodnje k skrajno zgornji plošči naboj Q; na krajnih ploščah verige se pojavita naelektritvi ±Q. In kaj se je med tem dogajalo na vmesnih ploščah? Plošči ob točki B sta eno, plošči ob točki C pa drugo nevtralno telo; za nevtralno telo pa že vemo, da se ob njegovi površini influira naboj, če se znajde v polju. Hkrati z elektritvijo krajnih dveh plošč verige in jačanjem električnega polja naboja teh plošč se dogaja tudi influenca v nevtralnih telesih, in sicer tako, da se prosti elektroni pomikajo k zgornjim ploščam; ti postajata vse bolj negativno, spodnji pa zato vse bolj pozitivno naelektreni. Proces influiranja je zaključen, ko sprejmeta spodnji plošči prvega in drugega kondenzatorja elektrino -Q, zgornji plošči drugega in tretjega pa pridobita nasprotno naelektritev Q. Zakaj ravno toliko? Šele takrat, ko bosta plošči vsakega kondenzatorja imeli ravno naboja ±Q, bo električno polje zunaj vseh kondenzatorjev enako nič, in ne bo več razloga, ki bi narekoval kakršnokoli dodatno influenco. Kaj je sklep? Po zaključenem elektrenju bodo naelektritve vseh kondenzatorjev enake, njihove napetosti pa bodo takrat: U₁ = Q / C₁, U₂ = Q / C₂, U₃ = Q / C₃. Razmerja med napetostmi bodo enaka razmerjem med recipročnimi vrednostmi kapacitivnosti:

Tu tiči razlog, da imenujemo verigo zaporedno vezanih kondenzatorjev tudi delilnik napetosti. Po zančnem Kirchhoffovem zakonu je napetost vira enaka vsoti napetosti kondenzatorjev:

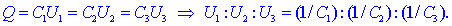
Vir spet »ne ve«, koliko kondenzatorjev je zares v verigi. Preselil je naboj Q, ki je tolikšen, kot če bi verigo nadomeščal ekvivalentni kondenzator, katerega kapacitivnost bi bila enaka nadomestni kapacitivnosti verige, C_nad. = Q / U; torej:
 

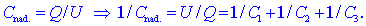
Od tu sledi formula: recipročna vrednost nadomestne kapacitivnosti več (n) zaporedno vezanih kondenzatorjev je enaka vsoti recipročnih vrednosti vseh kapacitivnosti kondenzatorjev v verigi,

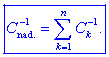
Zgled 4. V zanko povežimo kondenzatorje kapacitivnosti: C₁ = 2 mF, C₂ = 3 mF in  C₃ = 6 mF ter vir neznane napetosti U_x. Merilnik napetosti, volt-meter (V-m), izmeri na prvem kondenzatorju napetost 24 V. Določimo napetosti, naboje na kondenzatorjih in potenciale, če je spojišče D na potencialu nič voltov! Þ Napetost prvega kondenzatorja že poznamo: U₁ = 24 V. Naboj prvega in naboji vseh ostalih bodo enaki: Q = 24 V×2 mF = 48 mC. Od tu sledita napetosti: U₂ = (48/3) V = 16 V in U₃ = (48/6) V = 8 V. Napetost vira je enaka vsoti delnih napetosti, U_x = 48 V in nadomestna kapacitivnost je Q / U_x = 1 mF. Preverimo slednje še s formulo:

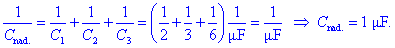
Potencial spojišča C je 8 V, spojišča B 24 V in spojišča A 48 V.

 
Kondenzator z večslojno izolacijo. Soroden primer zasledimo v ploščnem kondenzatorju z večslojno izolacijo; naj ima ta tri plasti (slika 8).

Vektor gostote pretoka določa naboja ±Q. Električni pretok je skozi vse tri izolante isti, poljske jakosti v njih pa so v splošnem različne:

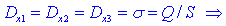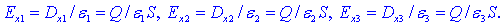
Celotna napetost je enaka vsoti delnih napetosti, kar dá pričakovan rezultat:
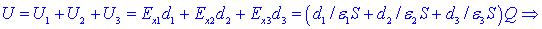
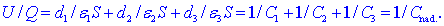