Magnetno polje v ravni dolgi tuljavi. Ravno tuljavo oblikuje N enakih spiralnih zavojev žice na valju; dolžina in srednji premer spirale sta l in d (slika 19).[1]

 Navitje takšne tuljave je po potrebi večslojno, s čimer se ustrezno poveča število ovojev na dani dolžini, poveča pa se tudi produkt NI, ki je odločilen za gostoto magnetnega polja. Poseben primer tuljave je ravna dolga tuljava; o njej govorimo, če je d << l. Pri dolgi tuljavi je magnetno polje v zunanjosti navitja v poprečju mnogo šibkejše od tistega v notranjosti. V osrednjem delu valja je vektor gostote magnetnega pretoka B usmerjen vzdolž osi Z in ima tam skoraj konstantno vrednost, ki jo določa komponenta[2]

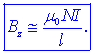
Z uporabo Biot-Savartovega zakona se da dobiti točno formulo, ki pa velja le za točke v osi tuljave in se glasi:

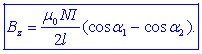
Kota a₁ in a₂, določa geometrija tuljave in lega točke T v osi (slika 20).

Izkoristimo priliko in formulo uporabimo pri ravni in dolgi tuljavi. Če nas zanima magnetno polje nekje v sredini tuljave, kjer je najmočnejše, je kot a₁ skoraj 0 °, kot a₂ pa skoraj 180 °. Razlika kosinusov kotov je približno 2, kar dá že znano formulo: B_z @ m₀NI / l. Iz predhodne enačbe tudi ni težko videti, da je magnetno polje ob konceh dolge tuljave le še polovica tiste v sredini. V točkah izven tuljave je gostota polja že občutno manjša.

Za boljšo predstavo magnetnega polja toka v ravni tuljavi navajamo sliko gostotnic, ki izhaja iz stroge uporabe Biot-Savartovega zakona (slika 21).

V sredini tuljave so gostotnice skoraj vzporedne črte (homogeno polje), ob konceh pa se redčijo, kar velja še toliko bolj v zunanjosti tuljave.

Zgled 6. Ravna tuljava naj ima 125 dotikajočih zavojev izolirane žice debeline 0,8 mm na tulcu premera 2 cm. Izračunajmo magnetno polje v sredini in na konceh tuljave, če je tok skozi žico 200 mA! Þ Dolžina tuljave je 125×0,8 mm = 100 mm. Izračunajmo gostoto magnetnega pretoka v sredini tuljave s približno formulo:

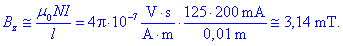
Nadaljujmo s točno formulo: izračunamo oba kosinusa

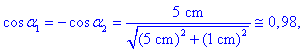
nadalje pa še

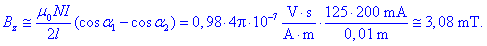
Točen rezultat je za dva odstotka manjši od približnega. Izračunajmo gostoto polja še ob koncu tuljave. Ob desnem koncu tuljave sta kosinusa takšnale:

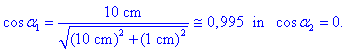
Gostota polja ob desnem (in enako tudi ob levem) ustju tuljave je

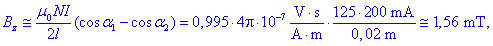
kar je približno polovica gostote v sredini tuljave.