Magnetno polje toka skozi toroidno navitje. Toroid je telo, ki ga »zariše« vrteča ploskev (slika 17).

Toroidna telesa so ovoj, prstan, venec, svitek, kolo in drugi. In kaj je toroidno navitje? To je spiralno navita žica na toroidu. Toroidno navitje navijamo, kot da bi »šivali«: žico povlečemo skozi odprtino toroida, ga z njo obvijemo in znova vbodemo in obvijemo, itn (slika 18).

Zavoji so po obodu običajno enakomerno razmeščeni; to navitje imenujemo toroidna tuljava. Poleg geometrije je podatek tuljave tudi število ovojev N.

Rezultančno magnetno polje toka skozi toroidno navitje ima nekaj lastnosti: 1) magnetno polje je »ujeto« v notranjost toroida,[1] 2) gostotnice magnetnega polja so krogi v toroidu, 3) smer magnetnega polja določa smer toka in desno pravilo in 4) vrtinčnost magnetnega polja na gostotnici je določena s tokom, ki ga ta objame. Vsaka gostotnica objame N-krat tok I, zato je produkt l_mB_t na krožni polmera r enak produktu m₀NI; iz tega sledi preprosta enačba:

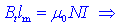
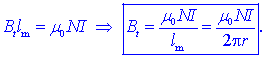
Izraz spominja na formulo za magnetno gostoto ob ravnem tokovodniku, le da vlogo toka I prevzame produkt NI. Resnično: magnetno polje B v toroidu je takšno, kot bi ga povzročal »namišljen raven vodnik« s tokom NI, ležeč v osi toroida. V enačbi se skriva še nekaj. Gostotnica se lahko dotika notranje stene toroida, kjer je radij r₁, ali pa zunanje stene, kjer je radij r₂. To pomeni, da je gostota pretoka ob notranji steni toroida večja od tiste ob zunanji steni:

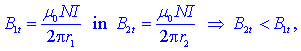
V praksi se pogosto opremo kar na srednji obseg oziroma na srednjo dolžino magnetne poti l_ms = 2pr_s v toroidu in na vrednost gostote magnetnega pretoka B_ts v sredini toroida,

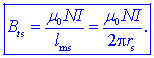
Zgled 5. Toroid ima kvadratni presek 2 cm ´ 2 cm in srednji polmer 5 cm. Na njem je navitje s 300 ovoji in tokom 20 mA. Izračunajmo največjo in najmanjšo gostoto ter gostoto magnetnega pretoka v sredini toroida! Þ Pišimo:
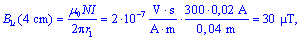
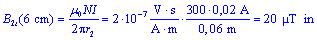