|
Magnetni pretok.
S pojmom pretoka skozi ploskev smo se srečali pri vektorjih
gostot J in D oziroma pri električnem toku i in
električnem pretoku fe;
in zakaj bi nekaj takega ne vpeljali tudi pri vektorju gostote
magnetnega pretoka B? Pretok vektorja B skozi ploskev
imenujemo magnetni pretok ali fluks, označujemo pa ga
s fm
oziroma f. Njegovega
pomena žal še ne prepoznavamo, vendar se bo izkazalo, da ima
pomembno vlogo pri temah, ki prihajajo naproti: pri delu magnetne
sile in pri inducirani napetosti, induktivnosti ter magnetni
energiji.
Definicija
magnetnega pretoka. Z gostotnicami upodabljamo smer vektorja
gostote magnetnega pretoka; prostori med njimi so kakor cevke (slika
1).
Magnetni pretok
Df
v cevki je enak produktu površine
DS prečnega preseka in absolutne vrednosti B
gostote magnetnega pretoka B na njem,
Df
= BDS.
Če nas zanima magnetni pretok f
skozi več sosednjih cevk, ga pridobimo z vsoto delnih pretokov
Dfk
= BkDSk:
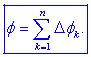
Namen risanja
pretočnih cevk smo utrdili že v prejšnjih poglavjih; tam rečeno
velja tudi za cevke magnetnega polja: kjer je cevka »stisnjena«, je
gostota polja večja, in obratno. Primerno bo, da si vprašanje
magnetnega pretoka ogledamo pri nekaterih tokovnih strukturah.
Magnetni pretok v
toroidni tuljavi. Magnetno polje toka I skozi toroidno
navitje z N ovoji smo že spoznali; zapisali smo tudi izraz za
gostoto Bts, ki se opira na vrtinčnost
in dolžino lms srednje gostotnice, Bts
=
m0NI
/ lms. Z njim moremo zapisati približek magnetnega
pretoka f v toroidu;
če ima ta presek S, ki je obenem prerez vseh cevk v toroidu
(slika 2), potem je:
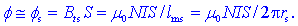
|