Magnetne lastnosti snovi.  Načine magnetiziranja magnetikov in polariziranja dielektrikov pojasnjujemo z modelom dipolov; ta je neke vrste stična točka modeliranja snovi v enem ali drugem v polju. Pri vrednotenju stopnje polariziranja snovi smo se oslonili na znano električno polje med ploščama naelektrenega kondenzatorja, kamor je bil vstavljen dielektrik, pri vrednotenju stopnje magnetiziranja snovi pa se bomo opirali na znano magnetno polje toka skozi toroidno navitje, med ovoje katerega bo vstavljen magnetik. Ob tem se bomo spoznali z novo količino, z vektorjem magnetne poljske jakosti, ki ima pomembno vlogo v magnetikih, vsebinsko pa se navezuje na tok prostih nabojev.

Ponovimo lepo lastnost vektorja gostote magnetnega pretoka B₀ toka I skozi toroidno navitje z N ovoji: polje B₀ je krožno in ujeto v toroid, smernost mu določa desno pravilo, njegova tangentna komponenta na srednji gostotnici, ki je hkrati tudi približek za srednjo gostoto magnetnega pretoka v toroidu, pa je določena z izrazom B_0t = m₀NI / l_ms (slika 1). [1]

Toroidna tuljava z jedrom. Če je žica navita na toroid oziroma jedro, ki je iz magnetne snovi, rečemo taki tuljavi toroidna tuljava z jedrom (slika 2).

Zaradi magnetnega polja toka I se bo jedro magnetiziralo. Njegovo magnetno stanje moremo predstaviti s tokovnimi zankami oziroma z magnetnimi dipoli, katerih magnetno polje B₁ je v jedru ponovno krožno, določa pa ga tangentna komponenta B_1t. V para- in feromagnetnih jedrih je polje B₁ usmerjeno vdolž polja B₀, v diamagnetnih pa v nasprotno smer. Rezultančno polje B = B₀ + B₁ je torej krožno, njegova tangentna komponenta pa je B_t = B_0t + B_1t. Glede na to, da tiči vzrok magnetiziranja jedra v magnetnem polju B₀, rečemo toku I v navitju preprosto kar magnetilni tok.

Linearno magnetenje. Stopnja, do katere se toroid magnetizira, je odvisna od magnetilnega toka in magnetne snovi, iz katere je jedro. Pri diamagnetnih in paramagnetnih jedrih, ki se šibko magnetizirajo, je rezultančna gostota B_t sorazmerna jakosti magnetilnega toka, pri feromagnetnih jedrih pa se izkaže, da velja sorazmernost med magnetno gostoto B_t in magnetilnim tokom I le v področju relativno majhnih vrednosti magnetilnih tokov, sicer ne; v prvem primeru govorimo o linearnem, v drugem o nelinearnem magnetenju. Jasne meje med njima ni, se pa na podlagi meritev stopnje magnetiziranja snovi izkaže, da je odvisna predvsem od nje same, posredno pa od dosežene gostote magnetnega pretoka v jedru. Pri večini feromagnetnih snovi je meja, ki ločuje prehod od linearnega v nelinearno magnetenje, okrog gostote enega tesla (neredko naletimo tudi na izjeme).[2] V začetku se bomo osredotočili na linearne magnetike oziroma na tiste snovi, ki se pri relativno majhnih magnetilnih tokih magnetijo skoraj linearno.

Relativna permeabilnost in permeabilnost snovi. Linearnemu magnetiku moremo stopnjo magnetiziranja ugotoviti s primerjavo med gostoto B_t v jedru in gostoto polja  B_0t v tuljavi, ki bi ne imela magnetnega jedra. Da bi mogli to stopnjo ovrednotiti, vpeljemo kvocient med gostoto B_t v jedru in gostoto B_0t v tuljavi brez jedra; imenujemo ga relativna permeabilnost m_r magnetika:

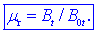
Relativno permeabilnost linearnih magnetnih snovi se določi empirično, torej z meritvijo (preglednica 1).

Iz razpredelnice razbiramo, da imamo opraviti praktično z le dvema vrstama magnetnih snovi: 1) dia- in paramagnetne snovi imajo relativno permeabilnost zelo blizu vrednosti ena, kar je posledica tega, da se te v magnetnem polju šibko magnetizirajo, pri prvih je m_r rahlo manjši, pri drugih pa rahlo večji od ena, 2) očitno drugačnost kažejo feromagnetiki in njihove zlitine, ki morejo imeti relativno permeabilnost tudi več stotisoč.[3] Za potrebe prakse bi bilo torej dovolj ločevati snovi zgolj na feromagnetne in vse ostale, ki so praktično nemagnetne in se vedejo kot prazen prostor.

Če se opremo na definicijo relativne permeabilnosti, potem sledi: 

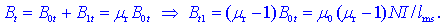
Enačba sporoča, da je magnetno polje Amperovih tokovnih zankic oziroma magnetnih dipolov v magnetiziranem feromagnetnem jedru lahko celo nekaj tisočkrat močnejše od magnetnega polja toka skozi toroidno navitje; in dalje: magnetno polje Amperovih zankic je v jedru takšno, kot da bi ga povzročal »nek tok I nevidnem navitju« z (m_r - 1)N ovoji. Zgornja enačba razkriva še eno zvezo:

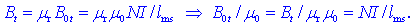
Iz nje izhaja tole: pri dani geometriji tuljave in magnetilnem toku I je gostota magnetnega pretoka v jedru premosorazmerna s faktorjem  m_rm₀. Če je jedro nemagnetno, je ta faktor enak permeabilnosti (m₀) praznega prostora oziroma vakuuma, sicer pa je m_r-kratnik permeabilnosti vakuuma. Ponuja se možnost, da magnetni snovi priredimo permeabilnost kot snovno lastnost na tale način:

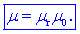
Vektor magnetne poljske jakosti. Nespremenljivost kvocienta med gostoto magnetnega pretoka in permeabilnostjo, B₀ / m₀ = B_t / m_rm₀, neglede na to, ali magnetno jedro v tuljavi je ali ga ni, nagovarja, da bi ta kvocient sprejeli kot novo količino, ki je pridružena h gostoti magnetnega pretoka in se navezuje na tok I magnetenja. Ta nova količina je v splošnem vektor, imenujemo pa jo vektor magnetne poljske jakosti H; v linearni snovi določa vektor H kvocient vektorja gostote magnetnega pretoka in permeabilnosti m  = m_rm₀ snovi:

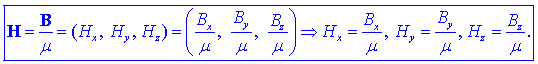
Vektor magnetne poljske jakosti H je torej vektor, ki je v prostoru sosmeren vektorju gostote magnetnega pretoka B (slika 3).[4]

Iz prejšnjih zvez sledi tudi tangentna komponenta H_t vektorja magnetne poljske jakosti H na srednji gostotnici v toroidu, 

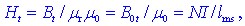
na drugih gostotnicah znotraj toroida pa je določena z enačbo H_t = NI / l_m, kar pomeni, da je ob notranji steni toroida največja, ob zunanji pa najmanjša.

Podobnost med vektorjema H in B. V linearni magnetni snovi sloni ta na zvezi B = mH, ki kot takšna velja tudi za magnetno polje v praznem prostoru, torej B = m₀H, o katerem je tekla beseda vse do prejšnjega razdelka. In kaj to pomeni? Pomeni, da bi mogli vse dosedanje izraze, ki so vsebovali vektor B, zamenjati z m₀H, vključno s tistimi, ki podajajo formule za izračune gostot magnetnega pretoka obravnavanih tokovnih struktur: od tokovodnika, ravne ali toroidne tuljave do tokovnega elementa. Za določitev magnetne poljske jakosti teh struktur bi bilo potrebno v izrazih opustiti permeabilnost praznega prostora in že bi dobili formulo za magnetno poljsko jakost, njeno smer pa bi, kot prej, določali po desnem pravilu. V primeru ravnega tokovodnika bi bila slika vektorjev magnetne poljske jakosti H povsem identična sliki vektorjev gostote magnetnega pretoka B (slika 4), njeno tangentno komponento H_t na krožnici polmera r pa bi določala formula

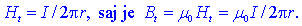
Povsem enako bi ravnali tudi pri formulah za magnetno polje v notranjosti vodnika, če je ta iz nemagnetne snovi (npr. Cu, Al in podobne), saj je njihova relativna permeabilnost enaka praktično permeabilnosti praznega prostora.[5]