Magnetna vezja. Beseda vezje zveni domače; nehote se spomnimo električnih vezij, bremen, virov, tokov, napetosti, pa tudi poti, ki nas je vodila do tja. Govorili smo o tokovnem polju, tokovni gostoti, električni poljski jakosti, Ohmovem zakonu, specifični električni prevodnosti, (ne)linearnosti, Kirchhoffovih zakonih idr. Priznati moremo, da smo nekaj sorodnih pojmov srečali tudi v magnetnetiki, in izgleda, da nas do magnetnega vezja ne loči več dolga pot.

Pojdimo po vrsti! V tokovnem polju smo pri (Ohmovem) linearnem zakonu upora imeli enačbo J =gE, pri linearnih magnetikih imamo enačbo B = mH; snovni konstanti povezujeta vektorja gostot z vektorjema jakosti. Magnetno enačbo bi utegnili preimenovati v »magnetni Ohmov zakon«, permeabilnost pa v nekakšno »specifično magnetno prevodnosti«. Če smo v tokovnem polju ugotovili, da je prevodni kanal večje prevodnosti ugodnejši za električni tok, potem bo feromagnetik večje permeabilnosti verjetno ugodnejši za magnetni pretok.

»Skok v magnetno vezje«! Zamislimo si jedro tuljave, ki ga oblikujeta dva linearna feromagnetna toroida (slika 1).

Preseka toroidov naj sta S₁ in S₂, njuni relativni permeabilnosti m _r1 in m _r2, srednja dolžina magnetne poti pa je v obeh enaka l_ms. Pri vzbujanju tuljave z magnetno napetostjo Q = NI bosta srednji vrednosti magnetnih poljskih jakosti v obeh delih jedra enaki (saj so gostotnice v obeh delih jedra še vedno krožnice, ki objemajo enako množino električnega toka). Zaradi različnih permeabilnosti delov jedra bosta srednji gostoti magnetnih pretokov B_1s in B_2s v njiju različni, zato bosta v splošnem različna tudi magnetna pretoka f₁ in f₂. Po že znanih izrazih iz predhodnega razdelka znamo njiju in celoten pretok f tudi zapisati, takole:

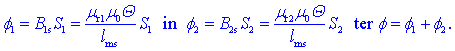
In že smo pri magnetnem vezju! Toroidno tuljavo, ki je vzbujana z magnetno napetostjo Q = NI, in delna pretoka f₁ in f₂ skozi jedri moremo predstaviti z zanko »vira magnetne napetosti« in vzporednih »magnetnih uporov«, katere  »magnetni tok« ustreza magnetnemu pretoku f v jedru tuljave (slika 2).

Simbol vira magnetne napetosti in simbol magnetnega upora si izposodimo iz električnih vezij, in enako tudi označevanje magnetnih tokov in magnetnih napetosti; »plus« pol vira je pri »sponki«, iz katere »izhaja« magnetni tok f.

Magnetna upornost. Magnetnemu vezju »manjka« le še opredelitev pojma »magnetna upornost«. Magnetno upornost R_m magnetnega kanala oziroma magnetnega upora določa kvocient magnetne napetosti in magnetnega toka; magnetni upornosti magnetnih poti sta:

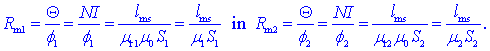
 Formuli spominjata na formulo za električno upornost prevodnega kanala in faktor m v imenovalcu nas utrjuje v misli, da je permeabilnost v vlogi svojske magnetne prevodnosti.

Drugačna magnetna jedra.  Glavnino časa smo posvetili toroidnim jedrom, v resnici pa jedra tuljav niso le takšna; izkoristimo priliko in se posvetimo še drugim oblikam feromagnetnih jeder! V ravnem tokovodniku je tok usmerjen vzdolž vodnika, če pa je ta zakrivljen ali zalomljen, se tej poti ukloni tudi tok. Glede na vlogo permeabilnosti (kot svojske magnetne prevodnosti snovi) moremo pričakovati, da bo v primeru lomljenega feromagnetnega kanala pot magnetnega fluksa skozi njega še vedno ugodnejša, kot pa skozi okoliški zrak (magnetni izolant) s permeabilnostjo m₀, ki je običajno tisoč- ali milijonkrat manjša od permeabilnosti feromagnetne snovi (slika 3).

Pomembno je še nekaj drugega! Pri visokopermeabilnih jedrih nikakor ni več potrebno, da so ovoji tuljave razmeščeni po vsem obodu, ampak so ti lahko zbrani le na delu jedra, kar samo tehnološko izvedbo tuljav z jedri precej poenstavi.[1]

 Ta spoznanja odpirajo možnosti snovanja magnetnih jeder, ki so prilagojena zahtevam in potrebam. V mislih imamo razvejana jedra z enim, dvema, tremi ali celo več navitji (slika 4).

Enozančno jedro z enim navitjem je dušilka,[2] enozančno z dvema navitjema je enofazni transformator, dvozančno jedro z dvema navitjema je varilni transformator in dvozančno s šestimi navitji je že trifazni transformator. Te in druge elektromagnetne strukture, kot so motorji, generatorji, elektromagneti, instrumenti, moremo v nadaljevanju modelirati z elementi magnetnih vezij in jih analizirati z metodami, ki smo jih spoznali pri električnih vezjih.

Modeliranje linearne magnetne strukture.  Izbiramo primer dvozančnega linearnega feromagnetnega jedra s permeabilnostjo m in presekom S, ki ima tri krake srednih dolžin l₁, l₂ in l₃, srednji ima še ozko zračno režo debeline d, in navitjema z N₁ in N₂ ovoji in tokoma I₁ in I₂. Pozornost vzbuja zračna reža, ki je tudi sestavina magnetnih struktur; največkrat je sicer neželena, včasih pa celo hotena. Feromagnetno jedro običajno ni odlitek, ampak je sestavljen iz paketov tanke pločevine, lamel (slika 5).[3]

Pri zlaganju lamel in paketov se pojavijo neželene reže; neizogibna je tudi med statorjem in rotorjem motorja. Reža more biti tudi hotena: da omogoči hod kotve (pomičnega dela jedra), ali da opredeli določeno karakteristiko naprave (takšno vlogo ima reža v izbrani dvozančni magnetni strukturi, ki predstavlja varilni transformator).[4] Magnetni pretok skozi zgornji in spodnji del srednjega stebra »prečka« torej tudi režo. Z vidika magnetnega vezja je reža v resnici dodaten upor. Magnetno upornost ji določa izraz, ki je soroden tistim za upornosti feromagnetnih poti po ostalih delih jedra:

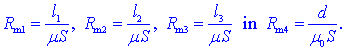
 Upori magnetnega vezja so s tem določeni; opredeliti moramo še vira. Njiju modelirata vira napetosti Q₁ = N₁I₁ in Q₂ = N₂I₂. Glede na smeri tokov I₁ in I₂ skozi vzbujalni navitji ter desno pravilo sta plus polariteti virov zgoraj; toka generirata magnetna pretoka v zgornje razvejišče krakov jedra. Vse povedano povzema modelno magnetno vezje. Od tu dalje se moremo lotiti analize vezja; pri tem uporabljamo metode za analizo električnih vezij.[5]

Zgled 1. V dvozančni magnetni strukturi s podatki, l₁ = l₂ = 30 cm, l₃ = 10 cm, S = 20 cm², d = 1 mm, m = 9000m₀, Q₁ = 100 A in Q₂ = 50 A, izračunajmo pretoke f₁, f₂ in f₃. Þ Najprej izračunamo magnetne upornosti:

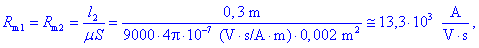
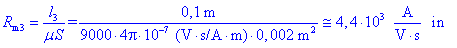
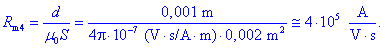
Izberimo metodo spojiščnih potencialov; virtualno potencialno izhodišče bodi v spodnjem spojišču. Izračunajmo magnetni potencial V_m zgornjega spojišča! Z njim izrazimo vse tri flukse:

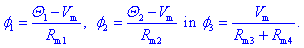
Po prvem Kirchhoffovem zakonu velja:

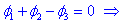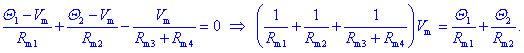
V enačbo zanesemo pripravljene podatke in dobimo: V_m @ 73,79 A. Od tu sledijo pretoki v stebrih:

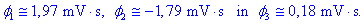
Opravila torej niso nič drugačna od tistih v električnih vezjih.

Nelinearno magnetno vezje. Analiza linearne magnetne strukture verjetno ni težavna (opiramo se na metode reševanja linearnih električnih vezjih), na težave pa naletimo, kadar je feromagnetno jedro nelinearno in so zaradi tega nelinearni tudi nekateri elementi magnetnega vezja (če se spominjamo, smo na podoben problem opozorili tudi pri nelinearnih električnih vezjih).[6] Da bi pa ne ostali zgolj pri tem, si oglejmo primer tuljave z jedrom, ki ima zračno režo (slika 6).[7]

Modelira ga enozančno nelinearno magnetno vezje, ki ga oblikujejo vir magnetne napetosti (tuljava), linearen upor (reža) in nelinearen upor (jedro). Magnetna napetost Q = Ni in lastnosti uporov določajo padca magnetne napetosti v jedru in reži, Q₁ in Q₀, ter magnetni pretok f skozi režo in jedro, kjer ima gostoto B=f / S.[8]  Magnetna napetost Q₁ je enaka produktu magnetne poljske jakosti H in dolžine magnetne poti l v jedru, napetost Q₀ pa je enaka produktu magnetne poljske jakosti B / m₀ in dolžine magnetne poti d v reži. Iz Kirchhoffovega zakona zanke sledi:

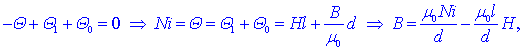
Zadnja enačba povezuje magnetno poljsko jakost in gostoto pretoka v jedru; prepoznavamo jo kot premico v diagramu B-H (slika 7);

abscisno os seka v točki (0, Ni / l), ordinatno pa v točki (0, m₀Ni / d). Nagib poševne premice je očitno neodvisen od jakosti toka i; ko bo magnetilni tok naraščal, bo premica drsela v desno, v nasprotnem v levo. Poleg tega pa sta H in B povezana tudi z magnetilno krivuljo, ki jo določa dinamika naraščanja in padanja toka. Kadar je jedro predhodno razmagneteno, za tem pa magnetilni tok i od vrednosti nič narašča, je potrebno premico vrisati v diagram, ki podaja začetno magnetilno krivuljo (slika 8).

Sečišče krivulje in premice, ki jo določa vrednost toka,  je delovna točka, ki pove, kolikšna sta B in H v jedru. Če pa je magnetilni tok izmeničen, je potrebno premico vrisati v diagram, ki podaja histerezo zanko. Pri naraščanju toka, je delovna točka na spodnjem delu, pri upadanju toka pa na zgornjem delu histerezne krivulje (slika 9).

Trajni magnet.  Za konec si omislimo primer magnetilnega toka, ki bi v času naraščanja od nič do največje vrednosti jedro z režo magnetil, v času usihanja do vrednosti nič pa bi ga delno razmagnetil. Ako je bilo jedro pred začetkom magnetenja razmagneteno in ima magnetilni tok še vrednost nič, leži poševna premica tako, da bi prečka izhodišče. V času naraščanja magnetilnega toka se premica pomika v desno, delovna točka pa drseti po začetni krivulji do točke »1«; v času upadanja toka se pomika delovna premica nazaj k izhodiščni legi, delovna točka pa drsi po zgornji krivulji do točke »2« (slika 10).

Magnetilni tok je od tega trenutka dalje enak nič; mogli bi si misliti, da takrat navitje odvijemo oziroma odstranimo; ostane zgolj delno namagneteno jedro z režo, trajni magnet. Zadnja delovna točka ima koordinati (H₂, B₂). Vrednost magnetne poljske jakosti v jedru je negativna:

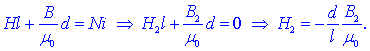
Jakost H₂ ustreza v resnici vrednosti tangentne komponente magnetne poljske jakosti H_2t na srednji gostotnici; to pomeni, da je vektor poljske jakosti H₂ v jedru usmerjen nasprotno od vektorja gostote magnetnega pretoka B₂. V reži je drugače: tam imata vektorja gostote magnetnega pretoka in poljske jakosti isto usmerjenost, saj ju veže zgolj permeabilnost praznega prostora. Enaka tangentna komponenta gostote magnetnega pretoka v magnetni zanki kaže na to, da jedro (tudi po prenehanju magnetilnega toka) zadrži določeno množino trajnega magnetnega pretoka f₂ = B₂S, ki je posledica zadržane usmerjenosti Weissovih domen oziroma magnetnih dipolov v jedru.

V praksi so trajni magneti seveda različnih oblik in različnih smeri zadržane magnetizacije; odvisno pač od potreb, ki to narekujejo; pogosti so podkvasti, ploščati in paličasti. Enozančno jedro z režo je primer podkvastega magneta. Če bi režo jedra (ob naraščanju in usihanju magnetilnega toka) zapolnjevala feromagnetna ploščica, ki bi jo po končanem procesu magnetenja izvlekli, bi dobili ploščat trajni magnet, če pa bi bilo jedro sestavljeno iz več delov, bi z njihovo razdružitvijo pridobili tudi več paličastih trajnih magnetov. Površino trajnega magneta, iz katere magnetno polje izstopa, imenujemo severni pol, nasprotno, v katero vstopa, pa južni pol.

Če paličast magnet (katerega gostotnice so podobne gostotnicam magnetnega polja ravne zračne tuljave) postavimo v neko magnetno polje (igla kompasa v Zemljinem magnetnem polju) in mu dopuščamo možnost vrtenja, potem se v njem obnaša tako kot tokovna zanka v magnetnem polju: zasuče se tako, da se magnetno polje Ampèrovih tokov v palici postavi v smer tistega polja.