Magnetni sili med tokovodnikoma. Uvodno temo namenjamo magnetnim silam med ravnimi vzporednimi tokovodniki. Če rišemo vodnik(e) v prerezu, označimo referenčno smer toka v list s »´« (krilcem puščice), iz lista pa s »·« (ostjo krilca). Če je, na primer, vrednost toka v list (papir) -5 A, potem je iz lista njegova vrednost 5 A (slika 1).

Začnimo kar s primerom dveh ravnih vzporednih vodnikov dolžine l, ki ležita na medosni oddaljenosti d in vodita enosmerna toka I in I₁ (slika 2).

Iz merjenj magnetne sile med njima sledi: 1) absolutni vrednosti sil na en ali drug vodnik sta enaki, 2) če imata toka isto smer, sta sili privlačni, v nasprotnem sta odbojni, in 3) absolutni vrednosti sil sta presorazmerni produktu tokov in dolžini vodnikov ter obratnosorazmerni z medosno oddaljenostjo. V mednarodnem merskem sistemu SI zapišemo absolutno vrednost magnetne sile takole:

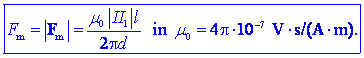
V izrazu je m₀ že znana konstanta, permeabilnost praznega prostora, ki ima v SI dano vrednost; ko jo vstavimo v zgornjo enačbo, dobimo formulo:

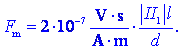
Zgled 1. Imejmo primer daljnovodnega dvojčka, para vzporednih vodnikov ene faze, ki vodita celoten tok 1000 A, vsak polovico, in sta v medosni razdalji 40 cm. Izračunajmo magnetni sili na vodnika na dolžini 300 m med stebroma daljnovoda! Þ Po vstavitvi podatkov sledi:

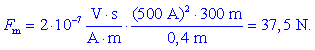
Zaradi istosmernosti tokov sta sili privlačni. Poleg vrednosti tokov je odločilna tudi dolžina vodnikov, zato je včasih primerneje izraziti silo v N na meter vodnika; v tem primeru je treba rezultat deliti s 300 m, kar da 0,125 N/m.

Definicija enote amper. Ponovimo definicijo ampera iz prvega razdelka: »Amper ali ampère je enota za električni tok. Amper je stalni električni tok, ki pri prehodu skozi dva premočrtna, vzporedna, neskončno dolga vodnika zanemarljivega krožnega prereza, postavljena v vakuum v medsebojni razdalji 1 m, povzroča med njima silo 2×10^-7 njutna na meter.«

V izraz za magnetno silo med tokovodnikoma vstavimo podatke,

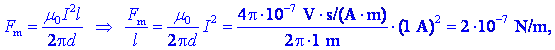
pa že dobimo to, kar sporoča definicija. Amper je torej (v resnici) izpeljana enota. Določena je s silo in razdaljo, če pa jo sprejemamo kot osnovno enoto, sledi iz definicije potrebna konstanta m₀ oziroma permeabilnost vakuuma, ki velikostno in dimenzijsko uskladi relacijo med silo, tokoma in oddaljenostjo.

Magnetne sile med vzporednimi ravnimi tokovodniki. Če bo vzporednih vodnikov več, bo sila na vsakega izmed njih seštevek delnih sil, ker pa je sila vektor, bo potrebno te vektorsko sešteti.

Zgled 2. Imejmo sistem treh vzporednih vodnikov, ki ležijo v skupni ravnini; prvi do drugega in drugi do tretjega so v oddaljenosti d = 1 m; toki so: I₁ = 200 A, I₂ = 400 A in I₃ = 200 A (slika 3).

Izračunajmo silo na desni tokovodnik na dolžini 50 m! Þ Srednji tokovodnik deluje na desnega odbojno, s silo v desno:

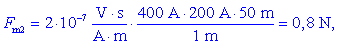
levi tokovodnik pa deluje na desnega privlačno, s silo v levo:

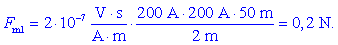
Rezultančna sila na tretji vodnik je usmerjena v desno in ima vrednost 0,6 N. Ni težko videti, da je tolikšna sila tudi na levi vodnik, vendar v levo, sila na srednjega pa je enaka nič, saj sta si magnetni sili zaradi stranskih dveh nasprotni.

Zgled 3. Imejmo spet te tri vodnike, vendar tokrat tako, da so eden od drugega oddaljeni za d = 2 m; v prerezni sliki ležijo v ogliščih enakostraničnega trikotnika (slika 4).

Izračunajmo silo na zgornji tokovodnik! Þ Prvi in tretji tokovodnik odbijata drugega od sebe s silama:

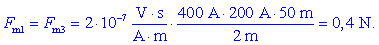
Sili sta enakih absolutnih vrednosti, vendar drugačnih smeri, oklepata kot 60 °; rezultančna sila je usmerjena navzgor, njena absolutna vrednost pa je:

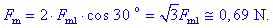
Gostota magnetnega pretoka. Seznanili se bomo z zelo važno količino magnetike, z gostoto magnetnega pretoka, ki je v zvezi z magnetno silo in ima pri njej enako pomembno vlogo, kot jo ima električna poljska jakost pri električni sili. Če je bil točkast naboj objekt, ob katerem smo govorili o električni sili, potem bo podobno vlogo v magnetiki prevzel tokovni element.

Tokovni element in magnetna sila. Ampère je bil zaslužen za hiter razvoj magnetike; njegovi eksperimenti so bili usmerjeni v iskanje tiste formule, ki bi omogočala izračun magnetne sile na katerikoli tokovodnik. V ta namen je izdelal vrsto naprav za merjenje magnetne sile na kratek raven tokovodnik, poimenovan tudi tokovni element (slika 1).

V nadaljevanju ga je zanimal primer le dveh tokovnih elementov oziroma sila na vsakega od njiju. Meritve so izpričevale, da je magnetna sila, delujoča na tokovni element, nanj vedno pravokotna, sicer pa sorazmerna produktu dolžin elementov in njunih tokov, obratnosorazmerna kvadratu oddaljenosti med njima in odvisna še od kotov, ki jih določajo smeri tokovnih elementov in zveznica med njima. Sliši se kar zapleteno, zato nadaljujmo po korakih.[1]

Vpeljimo dolžinski vektor Dl tokovnega elementa, ki naj ima smer označene smeri toka I v njem, in še produkt IDl, ki pomeni jakost tokovnega elementa. Z ozirom na ugotovljeno moremo za magnetno silo DF_m na tokovni element jakosti IDl izpostaviti dvoje: sorazmernost in pravokotnost (slika 2),

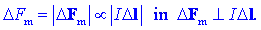
Ali najdemo kaj podobnega pri električni sili? Delno! Ugotovili smo, da je sila DF_e na delec z nabojem DQ, ki se nahaja ob drugem naboju, sorazmerna množini DQ in usmerjena vzdolž distančnega vektorja d med nabojema:

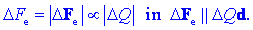
V nadaljevanju smo vpeljali vektor električne poljske jakosti E; z njim se sila na naboj DQ glasi: DF_e = DQE. Tudi v magnetiki bi bilo ugodno imeti vektor, ki bi pri množenju z IDl dal magnetno silo DF_m, delujočo na tokovni element. Glede na to, da je magnetna sila vedno pravokotna na tokovni element, more temu zadostiti kvečjemu vektorski produkt med jakostjo IDl in nekim novim vektorjem, imenovanim vektor gostote magnetnega pretoka B.[2] Z njim se sila DF_m na tokovni element jakosti IDl zapiše na tale način:[3]

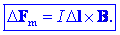
V izrazu imata svoje mesto jakost tokovnega elementa in magnetna sila, kar pomeni, da se v vektorju B »skriva« tisto, kar se tega tokovnega elementa ne tiče: to so drugi toki oziroma tokovni elementi. Nekaj takega smo povedali tudi o vektorju jakosti E: da se v njem odraža prisotnost ostalih nabojev, ki delujejo na naboj DQ s silo DF_e = DQE. Če smo se pri električni sili nadalje lotili določanja poljske jakosti elektrin v prostoru, potem bo tokrat naloga: določiti tokom lastna magnetna polja.

Magnetno polje ravnega tokovodnika. Izhajali bomo iz magnetnih sil med vzporednima tokovodnikoma; umestimo ju v koordinatni sistem (slika 3).

Vodnik s tokom I, naj leži v osi Z, vodnik s tokom I₁ pa vzporedno ob njem, na oddaljenost r, in sicer tako, da prebada list v točki P; toka skozi vodnika naj imata pozitivni vrednosti. Dolžini l₁ desnega vodnika priredimo vektor l₁ v smeri njegovega toka. Absolutno vrednost privlačne magnetne sile na desni vodnik zaradi levega že poznamo, po drugi strani pa iščemo še vektor B na mestu desnega vodnika, da bo vektor F_m izražen z vektorskim produktom:

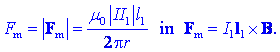
Naj je desni vodnik vzporedno premakljiv po krožnici s polmerom r iz P v točke Q, R, S, T in U (slika 4).

Magnetna sila na njega bo v katerikoli legi enake absolutne vrednosti, usmerjena pa vsakokrat k vodniku s tokom I: v P levo, v Q levo/navzdol, v R navzdol, v S desno/navzdol, v T desno in v točki U navzgor. Ta lastnost magnetne sile nas navaja na misel, da je vektor B »verjetno« tak, da je v točkah na krožnici pravokoten na vektor I₁l₁ in ima tam konstantno absolutno vrednost, da velja

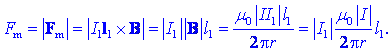
Če je tako, potem je absolutna vrednost vektorja gostote magnetnega pretoka na krožnici določena z izrazom
 

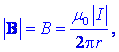
da jo določata tok in radij krožnice, medtem ko je smer vektorja B vsakokrat tista, ki dá v produktu I₁l₁ ´ B (po desnem pravilu) pravo smer sile F_m. Tej zahtevi zadostijo vektorji, ki so tangentni na krožnico in usmerjeni po desnem pravilu na tale način: če usmerimo pogled vzdolž označenega toka (kamor bi se pomikal vijak), se iz smeri vrtenja desnega vijaka dobi smer vektorja B (slika 5).

Projekcijo B_t vektorja B na tangentno os v točki na krožnici določa izraz

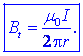
Tangentna projekcija vektorja gostote magnetnega pretoka B je sorazmerna vrednosti toka in obratnosorazmerna oddaljenosti od osi tokovodnika.

Ob dobljeni formuli se kaže spomniti njej podobne za radialno komponento vektorja električne poljske jakosti ob naelektrenem ravnem vodniku,

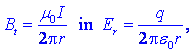
to še posebno, če se zavedamo, da ima vodnik, ki vodi tok I praktično vedno tudi neko naelektritev q. Ob takšnem vodniku bo električno polje radialno, magnetno polje bo krožno, med seboj si bosta pravokotni, z oddaljevanjem od vodnika pa se bosta manjšali obratnosorazmerno z radijem r (slika 6).

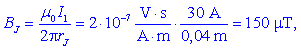
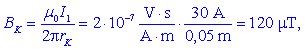
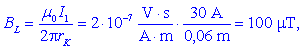
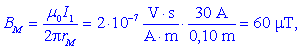
Zgled 1. Vodnik s tokom I1 = 30 A, usmerjenim v list, leži v osi Z (slika 7). Slika 7. Vektorji gostote magnetnega pretoka B v točkah ob ravnem tokovodniku. Izračunajmo absolutne vrednosti vektorja gostote magnetnega pretoka B v točkah J(4 cm, 0), K(3 cm, 4 cm), L(-6 cm, 0) in M(8 cm, -6 cm) ter jih upodobimo z usmerjenimi daljicami! Þ Absolutne vrednosti so: Pri upodabljanju vektorjev (ti dajejo vtis kroženja okrog osi vodnika v desno okrog smeri toka) bodimo pozorni tudi na dolžine, da v merilu ustrezajo vrednostim |B| v izbranih točkah.

Gostotnice magnetnega polja ravnega tokovodnika. Pojem gostotnic smo srečali že pri vektorjih tokovne gostote J in gostote električnega pretoka D ter povedali, da je njihovo risanje način, ki služi upodabljanju vektorskega polja. Glede na krožno naravo magnetnega polja okrog ravnega tokovodnika bodo gostotnice polja B kar koncentrični krogi (slika 8).

Ne bo odveč, če se ob tokovodniku, ko je še naelektren, spomnimo tudi silnic električnega polja. Gostotnice magnetnega in silnice električnega polja spominjajo na pajčevino: električno polje je radialno, magnetno pa je krožno na vodnik.