Magnetno odklanjanje.  Spoznali smo magnetno silo, vektor gostote magnetnega pretoka in magnetni pretok; to bo dovolj za ogled katere od uporab magnetne sile. Govorili bomo o gibanju naelektrenega delca v magnetnem polju, magnetnem odklanjanju, Lorentzovi sili in Hallovem pojavu.

Magnetna sila na gibajoč naboj. Izhajamo iz sile na tokovni element:

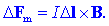
Tokovni element je kratek odsek tokovodnika, ki ga opredeljuje vektor IDl. V njem je določena množina naboja DQ, ki se giblje s hitrostjo v (slika 1).

Če je Dt časovni interval, v katerem se naboj DQ v celoti premakne v sosednji tokovni element, tedaj velja tole:

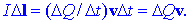
Rezultat je zelo zanimiv: jakosti tokovnega elementa ustreza produkt naboja in vektorja hitrosti, s katero se ta giblje. Resnično: magnetna sila ne deluje na vodnik kot tak, ampak na naelektrene delce, ki se v njem gibajo. To pomeni, da za nastop magnetne sile ni nujen vodnik: dovolj je že naboj, ki se giblje v vakuumu, zraku, tekočini ali kakem drugem mediju; končno tudi v vodniku. S tem se odpira možnost zapisa magnetne sile na posplošnen način:

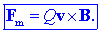
 Ob njem moremo reči: če se gibajoči delec znajde v magnetnem polju, deluje nanj magnetna sila, ki je enaka vektorskemu zmnožku »naboja-hitrosti« in vektorja gostote magnetnega pretoka.

 Iz lastnosti vektorskega produkta izhaja nekaj sporočil. Vektor magnetne sile je vedno pravokoten na vektorja hitrosti in gostote polja (slika 2).

Če se giblje delec vzdolž gostotnice magnetnega polja je sila nična, saj je vektorski produkt vzporednih vektorjev enak nič. V poosebljenem smislu bi rekli, da giban naboj »čuti« le tisti del vektorja magnetnega polja, ki je pravokoten na hitrost. Res je tudi dejstvo, da magnetno polje na mirujoč naboj ne učinkuje, da ga ne premakne z mesta (za razliko od električnega polja, ki pa to zmore).

Delec v magnetnem polju. Imejmo delec z nabojem Q in maso m v polju gostote B, ki se v trenutku t nahaja v točki T in ima tam hitrost v (slika 3).

Zaradi magnetne sile F_m = Qv ´ B bo njegovo gibanje v nadaljevanju pospešeno, s pospeškom a, ki ga (po drugem Newtonovem zakonu) določa kvocient sile in mase:

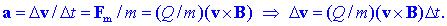
 Od tu sledi, da je sprememba Dv vektorja hitrosti vedno pravokotna na vektor hitrosti v. Enačba odstira tole: ker je v vsakem, tudi najkrajšem, intervalu Dt vektor Dv vedno pravokoten na v, se absolutna vrednost vektorja hitrosti v ne more spremeniti. Ali še drugače: delcu more magnetno polje spremeniti smer gibanja, ne more pa mu spremeniti absolutne vrednosti hitrosti (to sposobnost ima le električno polje). Pot delca v magnetnem polju bo zato neka krivulja: ob času t₁ bo v točki T₁ imel hitrost v₁, ob času t₂ bo v točki T₂ imel hitrost v₂, itn. Vektor hitrosti bo sicer vsakokrat drugačen, njegova absolutna vrednost pa bo ostajala nespremenjena, |v₁| = | v₂| = | v₃| =  ...  (slika 4).

Gibanje delca v homogenem magnetnem polju. Analiza gibanja delca v splošnem magnetnem polju ni enostavna naloga, zato se lotimo lažje, vendar vseeno pomembne: gibanja nabitega delca v homogenem magnetnem polju. Da bo magnetna sila različna od nič, moramo privzeti, da ima delec že neko hitrost v ¹ 0. Vektor te hitrosti razstavimo na tangentni (v_t) in normalni (v_n) vektor; prvi je vzporeden, drugi pa pravokoten na polje B (slika 5).

Če bi imel delec le vzporedni del hitrosti, bi bila magnetna sila enaka nič; delec bi se v takšnem primeru (prvi Newtonov zakon) gibal enakomerno premočrtno vzdolž gostotnice. Če pa bi delec imel le pravokotni del hitrosti, potem bi na njega delovala magnetna sila; pospešek in njegova absolutna vrednost bi bila:

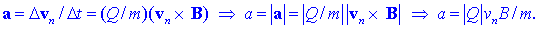
Glede na ugotovljeno, da se absolutna vrednost hitrosti delca v magnetnem polju ne more spremeniti, velja (zaradi zadnje enačbe) isto tudi za absolutno vrednost pospeška. Lastnosti, da se pri gibanju delca ohranja oboje, ustreza le enakomerno kroženje (slika 6); določiti nam je torej radij r, obhodni čas T oziroma frekvenco f in smer kroženja. Radialni pospešek je določen z enačbo a = v_n² / r, iz česar sledi radij:

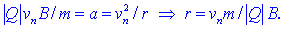
Pri vsakem obratu prepotuje delec pot 2pr, zato sta:

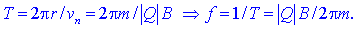
Pri določitvi smeri gibanja se opiramo na vektorsko enačbo za magnetno silo, ki je v vsakem primeru usmerjena v center kroženja. Pri usmeritvi polja B v list kroži pozitivni delec v levo, negativni pa v desno. Krožeča delca moremo predstaviti s krožno zanko in tokom I = |Q|f v levo, to pa zato, ker sta gibanji pozitivnega in negativnega delca v obratnih smereh (z vidika smeri toka) enakovredni. Lastno magnetno polje »inducirane tokovne zanke« ima na opni krožnice smer, ki je nasprotna gostoti B, ki jo je izzvala.

Zgled 1. V homogenem magnetnem polju gostote 1 T je pravokotni del hitrosti protona (m_p = 1,67×10^-27 kg) enak 10⁶ m/s. Þ  Radij in frekvenca kroženja sta:

 
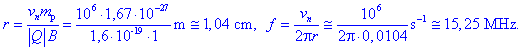
Brž ko bi imel delec tudi komponento hitrosti vzdolž magnetnega polja, bi tirnica ne bila več krožnica, ampak vijačnica (spirala ali heliks).

Magnetno odklanjanje. Za pojasnitev magnetnega odklanjanja si omislimo pas širine d, v katerem je homogeno polje gostote B (slika 7).[1]

Pravokotno v pas naj s hitrostjo v prileti delec z nabojem Q in maso m. Po vstopu v pas začne na njega delovati sila, ki ga povleče v kroženje z radijem r = mv / |Q|B. Glede na debelino pasu, predznak naboja in radij se »ponuja« več trajektorij. Polje odkloni pozitivni delec v levo, negativnega pa v desno. Delec preleti polkrožni lok in izstopi na isti strani, ali pa manj kot četrtinskega in izstopi na drugi strani ter se od tam oddaljuje enakomerno premočrtno.[2]

Odklanjanje s preletom skozi magnetni pas se uporablja v televizijski katodni cevi. Pospeševalni del je pri njej takšen kot pri osciloskopu, odklonskega pa tvorita tuljavi na grlu cevi; njuni magnetni polji usmerjata k zaslonu naravnan elektronski curek.

Hallov pojav.[3] Ta pojav bomo pojasnili na primeru ploščatega tokovodnika širine a, ki leži pravokotno v polju gostote B (slika 8).

Na proste elektrone (gibajoče s hitrostjo v) deluje v levo usmerjena magnetna sila -ev ´ B. Zaradi nje se ob levem robu traku pojavi presežek, ob desnem pa manko elektronov; presežka nabojev povzročita v traku električno poljsko jakost E_H, usmerjeno v levo, in magnetni nasprotno električno silo -eE_H, (E_H = -v ´ B), ki zaustavi selitev elektronov.[4] Absolutni vrednosti jakosti E_H ustreza produkt vB. Med roboma traku se vzpostavi električna oziroma Hallova napetost U_H = avB, ki je sorazmerna gostoti magnetnega pretoka B; ta lepa lastnost je osnova za instrument (Hallovo sondo), ki služi merjenju gostote magnetnega pretoka.[5]