|
Magnetni sklep.
Pri dosedanjih opravilih je pozornost (verjetno) pritegnila navada,
da smo razlagali indukcijo praviloma le v (enojni) zanki, v praksi
pa srečujemo mnogo bolj zamotane zavoje oziroma navitja. V to se
prepričamo, če odpremo elektromotor in se razgledamo po zavojih
žice, ki je vstavljena v utore statorja ali rotorja.
Mnogo bolj »urejeno«
navitje srečamo pri transformatorju, kjer je žica navita na
tuljavnik, ta pa je nataknjen na steber feromagnetnega jedra; v njem
naj se magnetni pretok časovno spreminja (slika 11).
Takrat se v vsakem
zavoju inducira enaka transformatorska napetost
-Df
/ Dt; ker pa si ti
sledijo drug za drugim, se napetosti, inducirane v posameznih (v
skupno N zavojih), seštejejo v rezultančno inducirano
napetost:
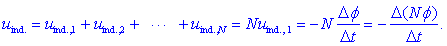
Iz končnega izraza bi
utegnili sklepati, da ima navitje en zavoj z fluksom Nf,
ne pa N zavojev s fluksom
f. Da bi različni
gledanji mogli nekako poenotiti, vpeljemo novo količino, imenovano
magnetni sklep y,
ki ni nič drugega kot magnetni pretok skozi navitje. Magnetni
sklep navitja je torej tista množina magnetnega pretoka, ki ga njeni
zavoji obkrožijo, inducirana napetost vzdolž njih v desno okoli tako
obkroženega pretoka pa je:
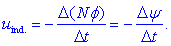
Razmišljanje vodi v posplošen
indukcijski zakon: inducirana napetost v zanki (ali navitju) v desno
okoli magnetnega pretoka je enaka negativni vrednosti strmine
magnetnega sklepa zanke (ali navitja):
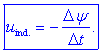
Zgled 5.
Transformatorja oblikujeta dve navitji na linearnem jedru srednjega
obsega l, preseka S in permeabilnosti
m
(slika 12).
Primarno navitje z N1
ovoji naj je harmonično vzbujano s tokom i1(t)
=
I1 cos (wt
+
a);
sekundarno navitje ima N2 ovojev. Izrazimo
napetosti med sponkama prvega in drugega navitja!
Þ
Najprej določimo magnetni pretok
f
v jedru:
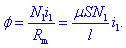
Magnetna sklepa prve in druge tuljave
sta:
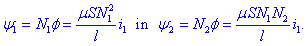
Za prvo navitje je to magnetni sklep
zaradi lastnega toka, zato bo tudi inducirana napetost v njej zgolj
posledica samoindukcije, za drugo navitje je to magnetni sklep
zaradi tujega toka, zato bo tudi inducirana napetost v njej zgolj
posledica tuje indukcije. Inducirani napetosti sta:
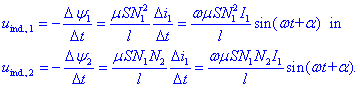
Inducirani napetosti sta si podobni: razlikujeta se
le v amplitudah, ki sta v razmerju števila ovojev. Na strani, kjer
je več ovojev, je večja tudi amplituda napetosti. Če v prvem navitju
zanemarimo padec napetosti zaradi njegove upornosti, je
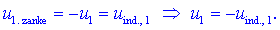
Pri drugem navitju je
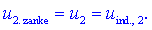
V
primeru, ko vsak zavoj navitja objema drugačen magnetni fluks,
je zapis inducirane napetosti nekoliko drugačen. Inducirana
napetost je takrat enaka vsoti induciranih napetosti v zavojih,
magnetni sklep pa je seštevek magnetnih pretokov skozi posamezne
zavoje:

|