Induktivnost tuljave.  V prejšnjem poglavju smo se ukvarjali z določanjem toku pridruženega magnetnega polja ob tokovodniku ali dvovodu in polja v tuljavah ter strukturah, ki jih sooblikujejo različna feromagnetna jedra. Kot zelo pogosto in dobrodošlo izjemo (ki pač ni pravilo) smo izpostavili lastnost linearnosti. Ta se kaže v tem, da so, tako gostota magnetnega pretoka kjerkoli v prostoru kot magnetni pretok f skozi katerokoli ploskev, po novem pa tudi sklep y oziroma množina z navitjem obkroženega pretoka, sorazmerni toku i, ki to polje povzroča. Kadar je linearnost strukture (zanke, navitja ali tuljave) zagotovljena, ji moremo prirediti količnik oziroma lastno induktivnost, ki jo definira kvocient magnetnega sklepa in toka:[1]

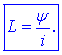
Imejmo tuljavo, katere toroidno jedro ima permeabilnost m. Magnetni pretok določa približna formula f = mSNi / l_ms (l_ms je srednji obseg jedra, S je njegov presek in N je število ovojev tuljave). Navitje tuljave objame magnetni pretok v jedru N-krat, zato je magnetni sklep y = Nf; iz definicijske enačbe dobimo njeno induktivnost,[2]

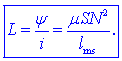
Zgled 1. Zračno toroidno navitje ima 500 ovojev; dolžina srednje gostotnice in presek toroida sta 40 cm in 10 cm². Izračunajmo induktivnost tuljave! Þ   Podatke zanesemo v formulo in dobimo:

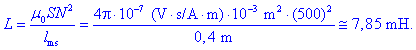
Tuljava z jedrom relativne permeabilnosti 10³ bi imela induktivnost 7,85 henrijev.

Ta preprosta formula zelo dobro ovrednoti tudi induktivnost tuljave, ki je na drugače oblikovanem enozančnem visokopermeabilnem jedru, nekoliko manj dobro pa induktivnost ravne tuljave z ali brez jedra (slika 1); dolžino l_ms v formuli zamenjuje takrat kar dolžina l navitja ravne tuljave.[3]

Induktivnost kot indukcijski koeficient. Imejmo zanko (navitje ali tuljavo) induktivnosti L. Tok i skozi zanko in napetost u med sponkama označimo na bremenski način; tako kot smo tega vajeni že tudi pri uporu ali kondenzatorju (slika 2).

Naj nam zaenkrat ni do »radovednosti«, v katero vezje je tuljava vključena, ampak bolj do iskanja soodvisnosti med napetostjo in tokom v luči indukcijskega zakona. Smer toka določa smer pretoka skozi zanko, pretok pa po desnem pravilu tudi smer inducirane napetosti. Zanka obkroži določeno množino pretoka, kar opredeljuje sklep zanke (glede na skorajda prekrivajoča zavoja, bi sklepali, da je y @ 2f).

 Če je upornost R žice zanemarljiva, potem je zanemarljiv tudi padec napetosti Ri, kar pomeni, da je napetost zanke v desno okoli magnetnega pretoka enaka ravno napetosti -u; ker pa je inducirana napetost enaka napetosti zanke, sledi:

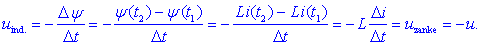
V zapisu smo upoštevali, da je induktivnost L zanke konstanta; zaradi tega se hitrost spreminjanja magnetnega sklepa prenese na hitrost spreminjanja toka. Iz zgornjega že sledi iskana zveza:

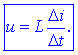
Relacija sporoča: napetost u med sponkama zanke je enaka produktu zankine induktivnosti L in hitrosti spreminjanja toka i skozi njo; induktivnost igra pri tem vlogo indukcijskega koeficienta. Enačba spominja na (nek način sorodni) enačbi, ki povezujeta napetost in tok na strnjenih elementih (kondenzatorju in uporu) in kar kliče po vpeljavi še enega strnjenega elementa električnih vezij, in sicer, tuljave.

Električni simbol tuljave. Niz polkrogov s črtma na konceh, ki ponazarjajo zavoje žice navitja s priključkoma, določajo simbol tuljave kot strnjenega elementa električnih vezij. Kot tak ni več snovno-geometrijski element, ampak zgolj idealen element; v celoti ga opredelijo oznaki napetosti in toka, induktivnost in enačba (slika 3).