Magnetna energija. Začnimo z idealno tuljavo induktivnosti L; ta naj je ali zračna ali z linearnim jedrom. Tok skozi njo in napetost med sponkama veže enačba u = L(Di / Dt). Izberimo najprej način magnetenja. Tok i skozi tuljavo naj je tak, da v času T narašča od vrednosti nič do končne vrednosti I, ki jo zadrži tudi še naprej; to nalogo more izvršiti tokovni funkcijski generator (slika 39-1). Razdelimo čas T na n intervalov trajanja Dt = T / n. Število n naj je tolikšno, da je Dt dovolj kratek oziroma primeren za določitev napetosti med priključkoma tuljave. Ob času t₀ = 0 s bo imel tok i vrednost 0 A, ob času t₁ = Dt vrednost i₁, ob t_k = kDt vrednost i_k in ob času t_n = T bo dosegel končno vrednost I. Poprečno napetost u_k med sponkama tuljave v k-tem intervalu določa strmina toka:

 Poprečna vrednost toka i je takrat enaka (i_{k + 1} + i_k) / 2. V tem času steče skozi vir določena množina naboja, ki je enaka zmnožku Dt(i_{k + 1} + i_k) / 2, pri tem pa vir opravi delo DA_gk, ki je enako zmnožku napetosti in naboja:

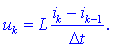
 Celotno delo A_g vira t₀ = 0 s do časa T je torej enako vsoti zaporednih del,

 Od časa t_n = T dalje je tok skozi tuljavo konstanten, napetost med sponkama tuljave oziroma vira je enaka nič in zato ta ne opravlja več nikakršnega dela.[1] Rezultat je preprost: delo vira določata induktivnost in končna vrednost toka, nič pa časovna oblika magnetilnega toka. Ko omenjamo magnetenje, mislimo seveda na magnetno polje tuljave, ki se je vseskozi krepilo, linearen magnetik pa magnetil.

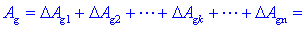
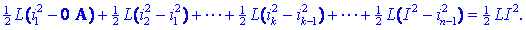
Če bi se tok vira od nekega kasnejšega časa T₁ manjšal do nič amperov, bi se proces v celoti odvrtel v obratni smeri. Zaradi manjšanja toka bi bila napetost u med sponkama vira oziroma tuljave vseskozi negativna, enako seveda tudi delo vira, kar pomeni, da bi vir energijo sprejemal (deloval bi v bremenskem režimu), tuljava pa bi energijo oddajala (bila bi v generatorskem režimu). Na koncu procesa razmagnetenja bi tuljava ne imela več toka, vir pa bi do takrat sprejel ravno toliko energije, kot jo je pred tem posredoval za magnetenje.

 Povsem očitno je magnetno polje tuljave nekaj takega, kot je električno polje kondenzatorja: da je tuljava sistem, ki je sposoben sprejemati in akumulirati magnetno energijo in jo kasneje oddajati in tudi scela oddati. Končna sprejeta magnetna energija je bila enaka LI² / 2, sicer pa je bila v tuljavi energija tudi ob vsakem drugem času (raz)magnetenja; njeno vrednost določajo tile izrazi:

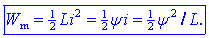
Akumulirana magnetna energija W_m je časovno odvisna količina; sorazmerna je kvadratu trenutne vrednosti toka skozi tuljavo. Tuljava je torej shranjevalec magnetne energije; kot takšen se pridružuje kondenzatorju, ki je shranjevalec električne energije. Čeravno smo ugotovili, da tuljava energijo tudi oddaja, da deluje takrat v generatorskem režimu, jo vseeno smatramo za pasivni element električnih vezij; saj ne (z)more oddati več energije, kot jo pred tem sprejme. 

Zgled 39-1. Skozi navitje tuljave induktivnosti treh henrijev je tok tristo ampreov. Kolikšna je v njej akumulirana magnetna energija? Þ  Račun je kratek:

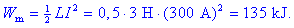
Gostota magnetne energije. Prav gotovo smo v elektromagnetiki že toliko udomačeni, da moremo predvidevati, da je magnetna energija tam, kjer je polje, in da je je v polju večje gostote več kot drugje. Spomnimo se toroidne tuljave; magnetno polje je med ovoji tuljave oziroma v jedru. Kaj dobimo, če energijo tuljave (z N ovoji) delimo s prostornino (Sl_ms) jedra:

 Pridobljeno je ravno gostota magnetne energije w_m, ki jo določajo količine, ki so odgovorne za polje v prostoru:

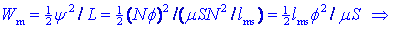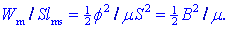
 Če primerjamo gostoti magnetne energije in električne energije, ugotovimo,[2]  da se zamenjajo vloge gostot (B, D), jakosti (H, E) in snovnih konstant (m, e). Pri določeni gostoti magnetnega pretoka je gostota magnetne energije v manj permeabilni snovi večja kot v bolj premeabilni. Lep primer je feromagnetno jedro z zračno režo, v kateri je gostota B enaka gostoti v jedru. Pri m_r = 1000 bi bilo v 1 mm reže ravno toliko energije kot je je v jedru dolžine 1 m.

Elektromagnet. Elektromagnet je elektro-mehanski pretvornik, ki izkorišča magnetno polje v reži za to, da izzove premik gibljivega dela feromagnetnega jedra ob reži. Imejmo podkvasto jedro z navitjem, ki ima upornosti R in je priključeno na vir enosmernega toka I, ob njem pa kotvo, ki je vpeta tako, da se more premikati k ali od podkve (slika 2).

Magnetna pot vzdolž podkve in kotve preseka S naj ima magnetno upornost R_m, vsota upornosti zračnih rež pa je 2d / m₀S. Zapišimo magnetni sklep v času t₁, ko je kotva na oddaljenosti d₁ od podkve, in magnetni sklep v kasnejšem času t₂, ko je ta do nje nekoliko bliže, npr. na oddaljenosti d₂:

Drugi sklep je večji od prvega, pa tudi magnetna energija v novem položaju je večja od tiste v starem:
 

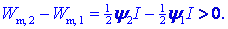
V intervalu Dt = t₂ - t₁ se je magnetni sklep navitja povečal, kar pomeni, da se je v tem času med sponkama inducirala napetost:

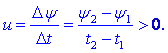
Kaj to pomeni? Vir, ki žene tok I skozi navitje in je imel pred premikom med sponkama napetost RI, je (zaradi premika) v intervalu Dt »doživel« povečanje napetosti in (poleg energije RI²Dt) oddal še del energije, ki je enaka

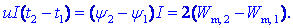
Vir je opravil še dodatno delo, ki je (po primerjavi z zgornjim izrazom) enako dvakratni spremembi magnetne energije. Polovica dela vira se je vgradila v povečanje magnetne energije. To drži, kje je potem še druga polovica? Ker ni drugih energijskih dejavnikov, se je morala iskana polovica nameniti delu za premik kotve! To pomeni, da je na kotvo delovala sila, magnetna sila F_m, sila magnetnega polja, ki je povlekla kotvo k jedru. Ta sila pa je enaka kvocientu dela in poti, zato je:

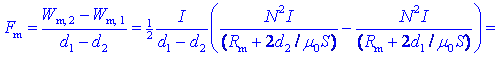
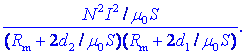
Verjetno je premik d₂ - d₁ v času Dt kratek, zato je d₂ @ d₁ = d, kar dá:

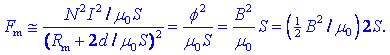
V oklepaju je gostota magnetne energije v režah, 2S pa je površina obeh rež. Na režah deluje na kotvo tlak f_m magnetne sile F_m, ki je enak

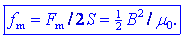
Pridobili smo pomembno enačbo: tlak na kotvo je enak kar gostoti magnetne energije v reži. Uporab magnetne sile ob režah je veliko: magnetna prijemala, magnetna stikala, kontaktorji, zvočniki, releji, in drugo. Nenazadnje bi mogli oceniti tudi silo, s katero se magnet v šahovski figuri »prisesa« na šahovnico. 

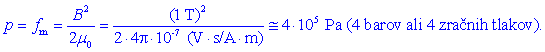
Zgled 3. Elektromagnet, ki »prijema« staro pločevino, da jo žerjav na odpadu prestavlja, ima površino rež 400 cm2. Ko žerjav položi elektromagnet na železno ploščo, ki je že tudi malo oksidirana (da je nekaj reže), in je v režah npr. gostota enega tesla, privlači ploščo s tlakom Reža preseka štirih kvadratnih decimetrov je dovolj za dvig plošče, ki ima težo do 16 kN, kar ustreza masi 1,6 tone. Če bi se elektromagnet dotaknil strehe avta, bi ga brez težav »držal«, žerjav pa prestavljal.