3.1.2 LASTNOSTI IN ZAKONITOSTI VZPOREDNE VEZAVE

KAZALO

    

 

 

3.1.2.3.4 Računanje z nadomestno prevodnostjo

      
 

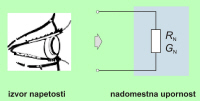
Izvor napetosti, ki požene tok skozi vzporedne porabnike, ne »čuti« vsakega porabnika posebej.

 

SLIKA

Slika 3.1.2.3.4.1: Nadomestna prevodnost (upornost) in nadomestni tokokrog

 

SLIKA

Slika 3.1.2.3.4.2: Nadomestno prevodnost gledamo iz izvora napetosti

 
       
 
►  

Tok izvora napetosti je, po Ohmovem zakonu, določen z napetostjo izvora in skupno prevodnostjo GN ali upornostjo RN porabnikov (sl. 3.1.2.3.4.1) ne glede na njihovo število.

  

 
       
 

Upoštevanje omenjenega dejstva poenostavi računanje v električnih tokokrogih z večjim številom porabnikov, v določenih primerih pa so problemi brez računanja s skupno upornostjo celo nerešljivi.

     
       
 
►  

Skupna prevodnost računsko nadomešča prevodnost vseh porabnikov, zato ji pravimo tudi nadomestna prevodnost.

  
►

Nadomestna prevodnost je prevodnost, ki jo čuti (»vidi«) izvor napetosti (sl. 3.1.2.3.4.2).

 
►  

Električnemu tokokrogu z nadomestno prevodnostjo, ki računsko nadomešča dejanski električni tokokrog s porabniki (sl. 3.1.2.3.4.1), pravimo nadomestni električni tokokrog.

  

 
       
 

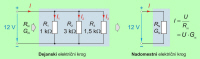
Poglejmo, kako si pri računanju električnih količin pomagamo z nadomestnim tokokrogom. Kot primer uporabimo vezavo vzporednih porabnikov (sl. 3.1.2.3.4.1), še prej pa se dogovorimo:

      
       
 
►  

Toke posameznih ali skupin vzporednih porabnikov bomo označili z indeksi porabnikov (I1, I2, I12, ... ).

  
►

Nadomestno prevodnost ali upornost vezave porabnikov bomo označili z indeksom »N« (GN, RN).

  
► Skupno prevodnost ali upornost dela vezave porabnikov bomo označili z indeksi teh porabnikov (G12, R12, ... ).  
►  

V primeru, da bodo vsi porabniki imeli enako prevodnost (upornost), jo bomo označili brez indeksa (G, R).

 

 
       
 

Vzporedne poti tokov (vodnih, prometnih, ... ) povečujejo prepustnost za tok v določeni smeri. Podobno velja za električni tok:

     
       
 
►  

Skupna prevodnost vzporednih porabnikov je enaka vsoti prevodnosti posameznih porabnikov.

  

 
       
 

G  =

G1 + G2 + G3 + ...

 (S) 
   
 

     Enačba 3.1.2.3.4.1

    
       
       ali tudi:    
       
 
1

RN
=
1
R1
 +
1

R2
 +
1

R3
 +
...
 (S)     R1(Ω); R2(Ω); … 
   
 

    Enačba 3.1.2.3.4.2

    
       
 

Obe enačbi lahko dobimo na enostaven način tudi računsko. Na osnovi dejanskega tokokroga vezave (sl. 3.1.2.3.4.1) lahko napišemo:

      
       
  I = I1 + I2 + I3 = U · G1 + U · G2 + U · G3 = U (G1 + G2 + G3)    
       
  Na osnovi nadomestnega tokokroga (sl. 3.1.2.3.4.1) lahko napišemo:    
       
  I = U · GN    
       
 

Ker sta levi strani enačb zadnjih zapisov toka I enaki, sta enaki tudi desni, odkoder lahko napišemo enačbo 3.1.2.3.4.1. Iz enačbe 3.1.2.3.4.1 lahko sklepamo naprej:

      
       
 
►  

Z naraščanjem števila porabnikov skupna prevodnost narašča in je vedno večja od prevodnosti posameznega porabnika.

 

 
       
  V primeru enakih upornosti porabnikov pa velja:    
       
 

GN =

n · G

 (S) n ... število vzporednih porabnikov
   
 

    Enačba 3.1.2.3.4.3

    
       
  Prevodnost in tok obravnavanega električnega tokokroga sta potem:    
 
GN=
1

1 · 103
+
1

3 · 103
+
1

1,5 · 103
=
3 + 1 + 2

3 · 103
=
6

3 · 103
= 2 · 10-3 S
    
  I = U · G = 12  · 2 · 10-3 = 24 mA