|
|
 |
|
 |
 |
 |
|
|
3.1.2.3.5 Računanje z
nadomestno upornostjo
|
|
|
|
|
|
|
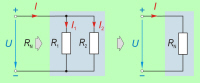
V vzporednih električnih tokokrogih je
enostavneje računati s prevodnostmi. Ni pa narobe, če
računamo z upornostmi. Za zgled izračunajmo najprej skupno upornost
prvih dveh porabnikov obravnavane vezave R1 in
R2 (sl. 3.1.2.3.5.1).
Na osnovi enačbe 3.1.2.3.4.2 lahko zapišemo: |
|
|
|
|
|
|
|
|
|
|
|
|
|
R1+ R2

R1
·
R2 |
|
| = |
| in od tod |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Enačba 3.1.2.3.5.1 |
|
|
|
|
|
|
|
|
|
|
► |
Skupna upornost dveh vzporednih porabnikov je določena s
kvocientom produkta in vsote upornosti porabnikov. |
|
 |
 |
|
|
|
|
|
|
|
|
|
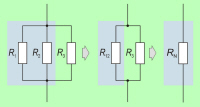
Če v vezavi na sl. 3.1.2.3.5.1 uporabimo namesto R1
in R2 njuno nadomestno upornost
R12
(sl. 3.1.2.3.5.2), lahko na osnovi enačbe 3.1.2.3.5.1 napišemo enačbo za
nadomestno upornost vseh treh vzporednih porabnikov: |
|
|
|
|
|
|
|
|
|
|
|
|
(Ω)
 |
|
|
|
|
|
Enačba 3.1.2.3.5.2 |
|
|
|
|
|
|
|
|
|
Enačba 3.1.2.3.5.2 omogoča postopno računanje
nadomestne upornosti na relativno preprost način, tudi v primeru
večjega števila vzporednih porabnikov. Če pa bi tudi v takem primeru
hoteli računati s končno obliko enačbe, bi jo dobili po enakem postopku
kot enačbo 3.1.8 tako, da bi upoštevali vse tri toke.
Dobili bi enačbo
3.1.2.3.5.3. |
|
|
|
|
|
|
|
|
|
|
| RN | = |
R1
R2R3

R1R2+R1R3+
R2R3 |
|
|
|
|
|
|
 |
 |
|
(Ω)   |
|
|
|
|
|
Enačba 3.1.2.3.5.3 |
|
|
|
|
|
|
|
|
|
|
► |
Skupna upornost treh vzporednih porabnikov je določena s
kvocientom produkta upornosti vseh treh porabnikov in
vsote produktov upornosti možnih kombinacij dveh
porabnikov.. |
|
 |
 |
|
|
|
|
|
|
|
|
|
|
|
 |
 Primer: Primer: |
 |
|
|
|
|
|
|
|
|
Iz pravkar izračunane skupne upornosti vzporednih
porabnikov pa razberemo še uporabno zanimivost, ki bo lahko
služila za kontrolo rezultatov računanja v podobnih primerih: |
|
|
|
|
|
|
|
|
|
|
|
► |
Skupna upornost vzporednih porabnikov je vedno
manjša od upornosti porabnika z najmanjšo upornostjo. |
|
 |
 |
|
|
|
|
|
|
|
|
|
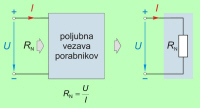
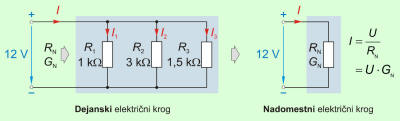
Če poznamo napetost in tok izvora, lahko določimo
nadomestno upornost ali prevodnost vseh porabnikov (slika 3.1.2.3.5.3), veliko
hitreje po Ohmovem zakonu: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(Ω) U(V);
I(A)  |
|
|
|
|
|
|
Enačba 3.1.2.3.5.4 |
|
|
|
|
|
|
|
|
|
|
|
V primeru enakih upornosti vzporednih porabnikov R pa bi
iz enačbe 3.1.2.3.4.3 dobili: |
|
|
|
|
|
|
|
|
|
|
|
|
GN = n
· G => |
1 |
|
= |
|
n |
|
· |
|
1 |
|
in od tod |
 |
 |
|
RN |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Enačba 3.1.2.3.5.5 |
|
|
|
|
|
|
|
|
|
|
|
|
► |
Nadomestna upornost vzporednih porabnikov enakih upornosti je
enaka kvocientu upornosti enega porabnika in
števila porabnikov. |
|
 |
 |
|
|
|
|
|
|
|
|
 |
 Primer: Primer: |
 |
|
|
|
|
|
|
|
|
 |
 Primer: Primer:
 |
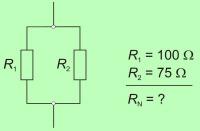
2. Porabnika iz primera 1 priključimo na izvor napetosti 12 V. Kolikšen
bo tok izvora?
|
I = U · GN = 12 · 0,0233 = 0,28 A |
|
 |
|
|
|
|
 |
|
|
|
|
|
|
|
|
|
 |
 Primer: Primer: |
 |
|
|
|
|
|
|
|
|
 |
 Primer: Primer: |
 |
|
|
|
|
|
|
|
|
|
|
   |
|
|
|
|
|
|
|
|