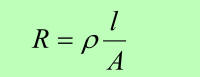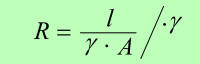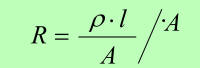|
|
 |
|
 |
 |
 |
|
|
2.4.1.3 Upornost in prevodnost
sta snovno geometrijski lastnosti vodnikov
|
|
|
|
|
|
|
|
|
SLIKA |
 |
|
 |
|
 |
|
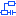
Slika 2.4.1.3.2: Plastni upor |
|
|
 |
|
SLIKA |
 |
|
 |
|
 |
|
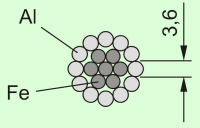
Slika 2.4.1.3.3: Prerez vodnika daljnovoda |
|
|
 |
|
|
|
|
Združimo vse tri ugotovitve o odvisnosti upornosti vodnika v eno: |
|
|
|
|
|
|
|
|
|
|
► |
Električna upornost je premo sorazmerna s specifično
upornostjo snovi in dolžino vodnika ter obratno
sorazmerna s prerezom vodnika. |
 |
 |
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Obratno velja za
prevodnost vodnika:
|
|
|
|
|
|
|
|
|
|
|
|
|
 |
|
 |
|
|
|
|
|
|
 |
 |
Kolikšna mora biti dolžina 0,3 mm debele žice iz konstantana, če naj
bo njena upornost 2,5 Ω?
| |
R |
|
= |
|
ρ |
|
· |
|
l |
|
 |
| A |
|
|
=> |
|
| |
l |
|
= |
|
R · A |
|
 |
| ρ |
|
| |
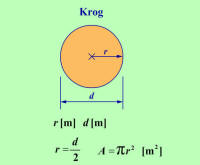
A = r2 ·
π = (0,15 · 10-3
m)2
· π = 0,07 · 10-6
m2 |
| |
l |
|
= |
|
R · A |
|
= |
|
2,5 Ω · 0,07 · 10-6
m2 |
|
= |
|
0,35 m |
|
= |
|
35 cm |
 |
 |
| ρ |
0,5 Ω · m · 10-6 |
Računanje prereza vodnikov.
|
 |
|
|
|
|
 |
|
|
|
|
|
|
 |
 |
Kolikšno upornost ima 30 m dolg bakreni vodnik s premerom 0,32 mm?
|
A
= |
| |
|
d
· π

4
|
|
|
| = |
| |
|
|
(0,32 · 10-3
m)2
· π

4
|
|
| = |
|
0,08 · 10-6
m2 |
|
R = |
|
ρ · |
|
l

A
|
|
|
| = |
| 0,018 · 10
-6 Ωm · |
|
|
30 m

0,08 · 10
-6 m2
|
|
| = |
|
6,75 Ω |
| |
|
|
|
 |
|
|
|
|
 |
|
|
|
|
|
|
 |
 |
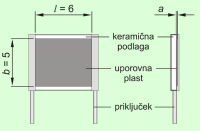
V razdelilni transformatorski postaji je za vodnik, ki povezuje
naprave velikih moči, uporabljen bakreni trak. Njegovo obliko in
dimenzije prikazuje sl. 2.4.1.3.1. Izračunaj upornost traku na označeni
dolžini!
| |
A = a ·
b = 60 · 10-3
m · 5 · 10-3 =
300 · 10-6
m2 |
|
R = |
|
ρ ·
|
l

A |
|
|
| = |
| 0,018 · 10
-6 Ωm · |
|
0,8 m

300 · 10
-6 m2 |
|
| = |
| 48 · 10 -6 Ω |
| = |
|
48 μΩ |
|
 |
|
|
|
|
 |
|
|
|
|
|
|
 |
 |
Upor, katerega upornost določa uporovna plast (sl. 2.4.1.3.2), mora
imeti upornost 100 Ω. Kolikšna mora biti debelina plasti, če je njena
specifična upornost 35 · 10
-6 Ωm?
| |
R |
|
= |
|
ρ |
|
· |
|
l |
|
 |
| A |
|
=> |
|
A = |
|
ρ · |
l

R |
|
|
| = |
|
35 · 10
-6 Ωm · |
|
6 · 10
-3 m

100 Ω |
|
| = |
|
2,1 · 10 -9 m2 |
| |
|
|
A = a · b =>
|
a = |
| |
A

b |
|
|
| = |
| |
|
2,1 · 10
-9
m2

5 · 10
-3 m |
|
| = |
|
0,42 · 10 -6
m = 0,42 μm |
| |
|
|
|
 |
|
|
|
|
 |
|
|
|
|
|
|
 |
 |
V zvitku imamo dvožilni kabel z bakrenima vodnikoma s prerezom 0,75
mm2. Na enem koncu kabla vodnika
staknemo, na drugem pa izmerimo njuni upornosti. Kolikšna je dolžina
kabla, če merilnik upornosti pokaže 0,92 Ω?
| |
R |
|
= |
|
ρ |
|
· |
|
l |
|
 |
| A |
|
=> |
|
l = |
| |
R · A

ρ |
|
|
| = |
| |
|
0,92 Ω · 0,75 · 10
-6
m2

0,018 · 10
-3 Ωm |
|
| = |
|
38,3 m |
Ker smo z opisanim načinom izmerili upornost obeh
vodnikov kabla (dvojna dolžina), je dolžina kabla enaka polovici
izračunane, torej 19,1 m. |
 |
|
|
|
|
 |
|
|
|
|
|
|
 |
|
 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Pri enostavnih električnih tokokrogih (gospodinjstva,
električne naprave, ...) je dolžina vodnikov najpogosteje do nekaj
metrov. Upornost vodnikov je v takšnih primerih relativno majhna in
jih v primerjavi z upornostmi porabnikov v večini primerov lahko
zanemarimo. Tok v tokokrogu računamo v takih primerih le na osnovi
napetosti na prIključnih sponkah izvora in upornosti porabnika. Obvezno
pa bomo upornost vodnikov morali upoštevati v električnih omrežjih in v
drugih primerih z daljšimi vodniki, s čemer se bomo seznanili v
okviru obravnave realnih električnih tokokrogov. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
  
|
|
|
|
|
|
|
|
|
|