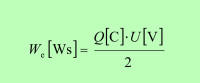4.3 ENERGIJA ELEKTRIČNEGA POLJA (W_e)

Številni poskusi pri obravnavi električnega polja so nas prepričali, da je v električnem polju shranjena določena energija. Kolikšna? Odgovor poiščemo pri naelektrenem ploščnem kondenzatorju, značilnem primeru homogenega električnega polja.

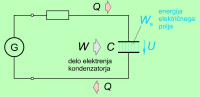
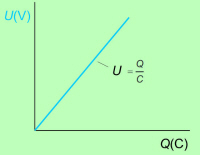
V naelektrenem kondenzatorju shranjena energija W_e je prav gotovo enaka delu polnjenja kondenzatorja W (sl. 4.3.1). To delo lahko izračunamo iz enačbe W = Q · U, toda pri tem moramo upoštevati, da delo W ni bilo opravljeno pri konstantni napetosti. Napetost na kondenzatorju namreč narašča premo sorazmerno z elektrino, ki doteka na kondenzator (sl. 4.3.2).

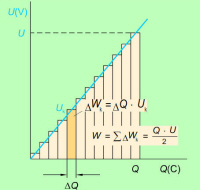
Zaradi lažjega razumevanja si polnjenje kondenzatorja zamislimo kot vsoto polnjenj z majhnimi koraki konstantne napetosti na način, kot ga prikazuje sl. 4.3.3. Za vsak tak korak velja enačba W_k = U_k · ∆Q , delo celotnega polnjenja pa je enako vsoti del posameznih korakov. Čim manjši so koraki, tem bližje smo linearnemu naraščanju napetosti in dejanski sliki odvisnosti energije električnega polja.

Enačba 4.3.1.
 

Elektrine kondenzatorja praviloma ne poznamo, zato na osnovi enačbe Q = C · U izvedemo uporabnejšo obliko enačbe za računanje energije električnega polja kondenzatorja:

Enačba 4.3.2.

Na podoben način kot smo dobili enačbo 4.3.2, lahko iz enačbe 4.3.1 dobimo še eno enačbo:

Enačba 4.3.3.

V električnem polju kondenzatorja ni shranjene ravno veliko električne energije. Toda če jo sprostimo v zelo kratkem času, dobimo kratkotrajno relativno veliko električno moč, ki zadostuje npr. za elektronski fotografski blisk, magnetenje trajnih magnetov, varjenje folij in podobno. Spreminjamo jo lahko tudi v mehansko energijo (elektrostatični merilniki, … ). Energija, shranjena v električnem polju, je torej pogosto prehodna oblika energije in osnova delovanja nekaterih pretvornikov energije.